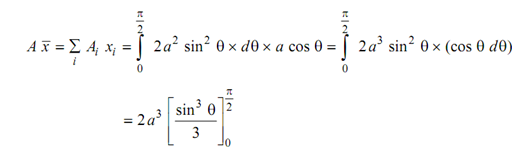Find out the centroid of an area of a semicircle:

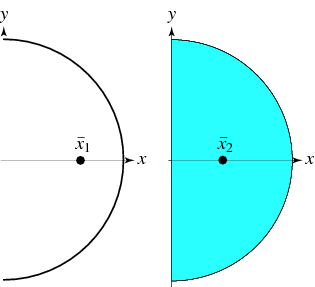
Find out the centroid of an area of a semicircle illustrated in Figure.

Solution

You shall note that it is not possible to divide a semicircle in a few appropriate standard-areas, for each of which magnitude with location of its centroid is known. Therefore, in such a condition, we should let a very large number of extremely thin strips of width dx and suppose that its centroid is at the centre of the strip.

Let the semicircle with the centre of the full circle at O, and its straight boundary EOD along with y-axis. Therefore, the axis OX is the axis of symmetry of the area. It means that the quadrant OEF is the mirror-image of quadrant OFD.

Let an elementary area such as a strip AB at a distance x from C with its width dx tending to zero. If a is the radius of semicircle

AB = 2 a sin θ

Elemental Area, where, dA = 2 a sin θ × dx

which gives,   x = a cos θ

dx = - a sin θ dθ

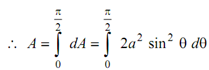                  (neglecting the -ve sign of dx)

Since      cos 2θ = 1 - 2 sin ²  θ

2 sin ²  θ = [1 - cos 2θ]

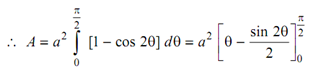
Since value of θ =  π/2 ,

∴ A = π a ² / 2

Which is already a known value of area of semicircle as area of full circle is (π a²); so one could have as well supposed it and proceeded as follows.

Letting the first moment of elemental areas about y-axis, we have

                                         ∴ (π a²/2 )x¯ =  2 a³ / 3

                                  ∴ x =  4 a /3 π ≈ 0.424 a = OG