Find out nature of position vector:

The position vector of a specific at any instant t with respect to the axes x, y and z is specified by

r (t ) = (4 t ²  + 5) i¯ + (3 t ²  + 2)j¯ + 0 k¯

Find out nature of its path and its position, velocity and acceleration at t = 3 seconds. Distances are measured in centimeters.

Solution         

As the coefficient of k in the given equation is zero, there is no displacement along z direction at any time t. This may be described as a motion of a particle in plane (XOY). If there is any coefficient for the k vector of the motion, the motion of the particle shall be in space.

The given equation of motion can be written as

x (t ) = 4 t ²  + 5,

y (t) = 3 t ²  + 2

 Eliminating t² from the above two relations, we obtain

t 2  = x - 5/4  = y - 2 / 3

∴ 3 x - 15 = 4 y - 8

∴ 3 x - 4 y - 7 = 0

The velocity and acceleration of the particle may be calculated from the relations

dx/ dt =  d /dt (4 t ²  + 5) = 8 t,             dy / dt =  d dt  (3 t ²  + 2) = 6 t

d ² x / dt ²  = 8,     d ² y/ dt ² = 6t

at         t = 3     v = 24 i¯ + 18 j¯

= 30 cm / sec. (that means)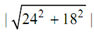

a = 8 i¯ + 6 j¯

= 10 cm / sec ² .