Find out all intervals where the given function is increasing or decreasing.

f ( x ) = - x⁵ + 5/2 x⁴ + 40/3 x³ + 5

Solution

To find out if the function is increasing or decreasing we will required the derivative.

f ′ ( x ) = -5x⁴ + 10x³ + 40x²

= -5x² ( x² - 2x - 8)

= -5x² ( x - 4) ( x + 2)

Note as well that while we factored the derivative first we factored a "-1" out to make the rest of the factoring a little bit easier.

From the factored form of the derivative we illustrates that we have three critical points :x = -2 ,x = 0 , and x = 4 .  We'll require these in a bit.

Now we have to determine where the derivative is +ve and where it's -ve..  As the derivative is a polynomial this is continuous and thus we know that the only way for it to change signs is to primary go through zero.

In other terms, the only place that the derivative might change signs is at the critical points of the function.  Now we've got another utilizes for critical points.  Thus, we'll build a number line, graph the critical points & pick test points through each region to illustrate if the derivative is positive or negative in each of region.

Following is the number line & the test points for the derivative.

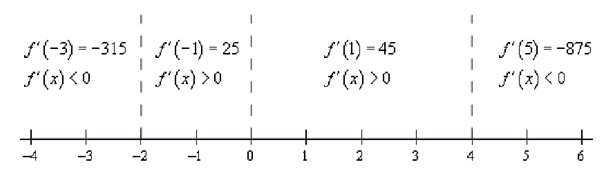
Ensure that you test your points in the derivative. Recall that we know that the derivative will be the similar sign in each of region. The only place that the derivative can alter signs is at the critical points & we've marked the only critical points onto the number line.

Thus, it looks we've got the given intervals of increase & decrease.

Increase : - 2 < x <0 and 0 < x < 4

Decrease : - ∞ < x < -2 and 4 < x < ∞