Draw shear force diagrams for the overhanging beam:

Draw shear force & bending moment diagrams for the overhanging beam illustrated in Figure

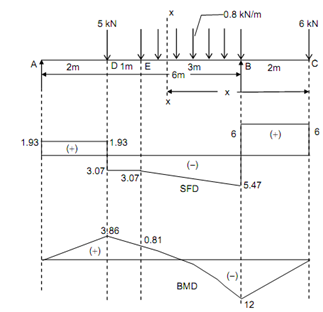
Figure

 Solution

Taking moments around A & equating to zero,

R_B   × 6 - (6 × 8) - 0.8 × 3 × ( 3 +(3/2))  - (5 × 2) = 0

R_B = 11.47 kN and R_A = 5 + (0.8 × 3) + 6 - 11.47 = 25 - 11.5 = 1.93 kN

Shear Force (beginning from the left end A)

SF at A, F_A = + 1.93 kN

SF just left of D, F_D = + 1.93 kN

SF just right of D, F_D = + 1.93 - 5 = - 3.07 kN

SF at E, F_E = - 3.07 kN

SF just left of B, F_B = - 3.07 - (0.8 × 3) = - 5.47 kN

 SF just right of B, F_B = - 5.47 + 11.47 = + 6 kN

SF just left of C, F_C = + 6 kN = Load at E

Bending Moment

BM at C, M_C  = 0

BM at B, M_B = - 6 × 2 = - 12 kN m

 BM at E, M _E =+ (11.46 × 3) - (6 × 5) -( 0.8 × 3 × (3/2) )=+ 0.81 kN m

BM at D, M_D = + 1.93 × 2 = + 3.86 kN m

BM at A, M_A = 0

Maximum Bending Moment

Maximum positive bending moment take place at D and maximum negative bending moment take place at B.

M_max (positive) = + 3.86 kN m

M_max (negative) = - 12 kN m

Point of Contraflexure

As the bending moment changes sign among E and B, let a section XX among E and B at a distance x from C.

BM at section XX,

M_x = - 6x + 11.47 (x - 2) - 0.8 (x - 2) ((x - 2)/2)

= - 6x + 11.47x - 22.94 - 0.4 (x - 2)²

= - 0.4x² + 7.07x - 24.54

By equating this equation to zero, we achieved the point of contraflexure,

- 0.4x² + 7.07x - 24.54 = 0

x² - 17.67x + 61.35 = 0

Solving out by trial and error,

x = 4    Value of (x² - 17.675x + 61.35) = 6.65

x = 4.9 Value of (x² - 17.675x + 61.35) = - 1.2475

x = 4.8  Value of (x² - 17.675x + 61.35) = - 0.45

x = 4.7 Value of (x² - 17.675x + 61.35) = 0.3675

 x = 4.75 Value of (x² - 17.675x + 61.35) = - 0.04375        

x = 4.745 Value of (x² - 17.675x + 61.35) = - 0.00285

Point of contraflexure is at distance of 4.745 m from the end of C.