Determine the wire diameter of the inner spring:

In a compound helical spring, the inner spring is arranged in and concentric with the outer one, but is 10 mm shorter. The outer spring contain 10 coils of mean radius 12 mm, and the wire diameter is equal to 3 mm. Determine the stiffness of the inner spring if an axial load of 150 N causes the outer one to compress 20 mm.

If the radius clearance among the springs is 1.5 mm, determine the wire diameter of the inner spring when it has 8 coils. G = 80 GPa.

Solution

Springs are in Parallel

Load carried by outer spring :

 Δ1 = 64 W₁ R³ n / Gd ⁴

=64 × W  × 12³× 10 / 80 × 10³ × 3⁴

∴          W₁ = 117 kN

Load carried by inner spring, W₂ = 150 -117 = 33 N

 Compression, Δ₂  = 20 - 10 = 10 mm

Stiffness, K₂   = 33/10 = 3.30 N/mm

Δ₂ =64 W₂ R³ n/ Gd ⁴

= 64 × 33 × (9 - 0.5 d )³ × 8 / 80 × 10³ × d ⁴

 ⇒        (18 - d )³  = 379 d ⁴

As d is small compared with 18, for a first approximation:

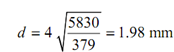
Second approximation

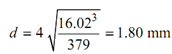
Third approximation

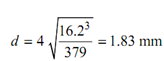
Fourth approximation

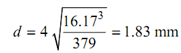
∴ d = 1.83 mm