Submit your working in (neat) handwritten form (do not type up your solutions). For the plots that you generate in Maple or Matlab, you can print them out and attach them at the end or cut them out and stick them in. Either way, make sure they are labelled properly.

It is OK to discuss these questions with other students, but the written version of this Problem Solving

Task must be your own. It is not OK to copy another student's work.

1. Use the method of Stationary Phase to determine the leading order term in the asymptotic expansion as k → ∞ for the integral

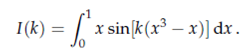
2. Consider the integral

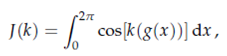
where

g(x) = x + 2 cos(x/2).

(a) Use Maple or Matlab is similar to plot cos[k(g(x))] over the domain [0, 2p] for each of

k = 2, 10 and 50.

(b) Find the point in [0, 2p] at which g0(x) = 0, and write out g(x) as a Taylor expansion about this point, including the first two non-zero terms (show all working, calculating derivatives by hand).

(c) Call the two-term Taylor expansion h(x), and plot h(x) over the domain [0, 2p] for each of k = 2, 10 and 50.

(d) Use the method of Stationary Phase to determine the leading order term in the asymptotic expansion of J(k) as k →∞.