Trapezoid Rule - Approximating Definite Integrals

For this rule we will do similar set up as for the Midpoint Rule. We will break up the interval [a, b] into n subintervals of width,

Δx = b - a / n

After that on each subinterval we will estimated the function with a straight line that is equivalent to the function values at either endpoint of the interval.  Now here is a sketch of this case for n = 6.

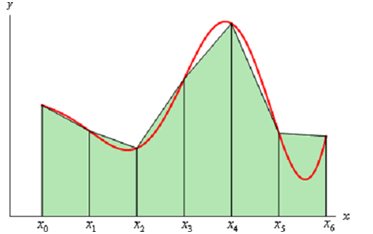
Every object in this is a trapezoid (therefore the rule's name...) and like we can see some of them do a very good job of approximating the actual area within the curve and others don't do such a good job.

The area of the trapezoid in the interval [x_i-1, x_i] is given by,  

A_i = Δx/2 (f (x_i-1) + f (x_i))

So, if we employ n subintervals the integral is just about,

∫^b_a f(x) dx ≈ Δx/2 (f (x₀) + f (x₁)) + Δx/2 (f(x₁) + f (x₂)) +.....+ Δx/2 (f (x_n-1) + f (x_n))

On doing a little simplification we reach at the general Trapezoid Rule.

 ∫^b_a f (x) dx ≈ Δx/2 [f (x₀) + 2f (x₁) + 2f (x₂) + .... + 2f (x_n-1) + f(x_n)]

Note: all the function evaluations along with the exception of the first and last, are multiplied by 2.