Determine reactions force:

Three sphere A, B and C weighing 400N, and 200N and having radii 400mm, 600mm and 400mm respectively are placed in trench as shown in the figure given below. Treating all contact surfaces as smooth, determine reactions developed

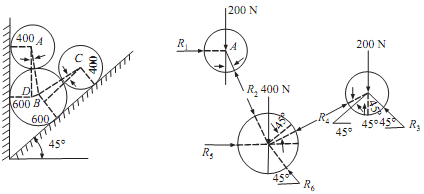
.: From the figure given below

Sinα   = BD/AB = (600 - 400)/(400 + 600) = 0.2

= 11.537° Referring to FBD of sphere A (Fig a)

R₂cosα  = 200

R₂  = 200/cos11.537° = 204.1 N         .......ANS

And R₁  - R₂sinα    = 0

R₁  = 40.8N                                               .......ANS

Referring to the FBD of sphere C,

Sum of forces parallel to the inclined plane = 0

R₄cosα  - 200cos45° = 0

R₄  = 144.3 N                                           .......ANS

Sum of forces perpendicular to the inclined plane = 0

R₄cos(45 -α  ) - R₃cos45° = 0

R₃  = 170.3N                                             .......ANS

Refer to FBD of cylinder B (as shown in figure)

V = 0

R₆sin45° - 400 - R2cos   - R4cos (45 + α   ) = 0

R₆sin 45° = 400 + 204.1 cos11.537° + 144.3cos56.537°

R₆ = 961.0 N                                           .......ANS

H = 0

R₅  - R₂sin   - R₄sin (45 +α   ) - R₆cos45° = 0

R₅ = 204.1 sin11.537 + 144.3sin56.537 + 961.0cos45°

R₅ = 840.7 N                                           .......ANS