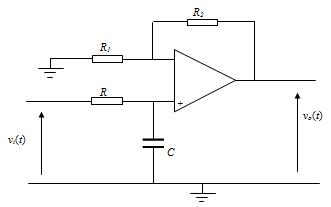
The circuit diagram of an active filter is shown below.

(a) Determine an expression for the transfer function of the filter.

(b) Hence find an expression for the frequency response of the filter.

(c) Calculate the ratio R1/R2 when low-frequency gain of the filter is 40 dB.

(d) Calculate R and C such that the break frequency on the Bode plot occurs at w0 = 500rad/s, (suggest commercially available values).

(e) For the values of the components obtained in parts (c) and (d) simplify the transfer function of the filter.

(f) Hence, using inverse Laplace transform, find h(t), the unit impulse response of the system.

(g) If the input to the filter is v_i(t)=10e-100t find an expression for the output of the system.

(h) For the input v_i(t)=1/√2 cosθ, obtain an expression for the steady-state sinusoidal response of the filter. 

Practical work

1.  Invoke MATLAB.

2.  The enclosed m-file is a MATLAB program that simulates the above problem.  In a new m-file type in the entire commands in the m-file

3.  Save the m-file, giving it a suitable file name.

4.  In MATLAB command window execute the program by typing its file name.

5.  If you have made no typing error(s), you should obtain a plot of the Magnitude and the Phase of the Frequency Response of the filter.

6.  Use the Bode plot for the magnitude and phase of the frequency response and measure and calculate the gain and phase for the input signal vi(t) = 1/√2 cos(500t), hence (i.e. using these measured values) write down an expression for the output of the filter.

7.  Verify that your measurements from the plots are in agreement with what you have found theoretically.  Comment with reason(s) if they do not agree.

8.  If the input to the filter is vi(t) =3 sin(2000 t), then what is an estimated expression for the output of the filter?  Write it down and explain how you came up with this answer.