Deflection at the centre - maximum deflection:

A simply supported beam of span 6 m is subjected to Udl of 24 kN/m for a length of 2 m from left support. Discover the deflection at the centre, maximum deflection & slopes at the ends and at the centre. Take EI = 20 × 10⁶ N-m².

Solution

∑ F_y  = 0, so that R_A  + R_B  = 24 × 2 = 48 kN          --------- (1)

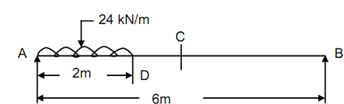
Taking moments around A,

24 × 2 × 1 = R_B  × 6

R_B  = 8 kN (↑)                     -------- (2)

R_A  = 48 - 8 = 40 kN (↑).         ------------(3)

By apply the Udl over the portion DB downwards and upwards,

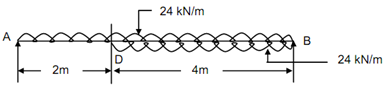
Figure

M = 40 x - 24 x × (x/2) + 24 ( x - 2) ( (x - 2)/2)

Note down that the third term vanishes if x < 2 m.

= 40 x - 12 x²  + 12 ( x - 2)²               ------- (4)

EI d ² y/ dx² = 40 x - 12 x ²  + 12 ( x - 2)²          ------- (5)

EI dy / dx = 40 x²/2- 12 x³ /3+ 12 ( x - 2)³/3 + C₁

= 20 x² - 4 x³ + 4 ( x - 2)³ + C₁           -------- (6)

EIy = 20 x ²/3 - x⁴ + (x - 2)⁴ + C₁ x + C₂            -------- (7)

Here again note that the third term vanishes for x < 2 m.

at A,      x = 0,    y = 0  ∴ C₂  = 0

at B,  x = 6 m,     y = 0         

0 = 20 × 6³ /3 - 64  + (6 - 2)⁴ + C₁ × 6

C1 =- 20 × 12 + 36 × 6 - ((16 × 16 )/6)=- 200/3

∴          EI dy/dx = 20 x²  - 4 x³  + 4 ( x - 2)³  - 200/3         -------- (8)

The third term vanishes.

Slope at A, (x = 0),     27

θ_A  = -200/3EI =- (200 × 10³)/ (3 × 20 ×10⁶)

            = -(1/300) rad = - 3.33 × 10^{- 3}  rad

Slope at B, (x = 6 m),

EI θ _B = 200 × 6²  - 4 × 6³  + 4 (6 - 2)³  - (200/3)

 θ  = 136/ 3 EI = (136 × 10³ )/(3 × 20 ×10⁶)

= + 2.27 × 10^{- 3}  radian

Slope at C, (x = 3 m), i.e. x > 2 m

EI θ _C = 20 × 3²  - 4 × 3³  + 4 (3 - 2)³  - (200/3)

θ_C = 20 /3 EI = 0.47 × 10^{- 3}  radians

EIy =( 20 x ³/3)- x⁴  + ( x - 2)⁴  - (200/3) x                   -------- (9)

Deflection at centre, (x = 3 m),

EIy_C = (20/3) × 33  - 34  + (3 - 2)4  - (200 /3)× 3

y_C  = - 100 / EI =  - 100 × 10³ × 10³ / (20 × 10⁶)

= - 5 mm

For maximum deflection,

dy/ dx  = 0

0 = 20 x²  - 4x³  + 4 ( x - 2)³  - (200/3)

= 20 x²  - 4x³  + 4x³  - 32 - 24 x²  + 48 x - (200 /3)

=- 4x²  + 48 x - (296 /3)

∴          x2  - 12x + (74 /3 )= 0

x = 2.63 m , x > 2m

EIy _max = (20/3) × 2.633  - 2.634  + (2.63 - 2)4  - (200/3) × 2.63 = - 101.7

∴ y_max  = - 5.087 mm;  - 5.1 mm