Definition of Relation

A relation is a set of ordered pairs.

It seems like an odd definition however we'll require it for the definition of a function though, before actually we give the definition of a function let's see if we can get a handle on just what a relation is.

In example we constructed a set of ordered pairs we used to sketch the graph of that we used.

                            y =( x -1)²  - 4

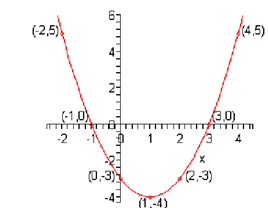
Here are the ordered pairs of this graph

( -2, 5)( -1, 0)(0, -3)(1, -4)(2, -3)(3, 0)( 4, 5)

Thenany of the following are relations since they consist of a set of ordered pairs.

{( -2, 5)  ( -1, 0)  ( 2, -3)}

{( -1, 0)  (0, -3) ( 2, -3)  (3, 0)  ( 4, 5)}

{(3, 0)  ( 4, 5)}

{( -2, 5)  ( -1, 0)  (0, -3) (1, -4)  ( 2, -3)  (3, 0)  ( 4, 5)}

Of course there are several more relations which we could make from the list of ordered pairs above, however we just desired to list a few possible relations to give some instance.  Notice as well that we could get other ordered pairs also from the equation and add those into any of the relations above if we desired to.

Now, at this point you are possibly asking just why we care about relations & that is a good question. Some relations are extremely special and are utilized at almost all levels of mathematics. Given definition tells us just which relations are these special relations.