See the Petri net represent in following figures (a) and (b) as represented in the figure for analysis and depiction of qualitative pathological behaviors.
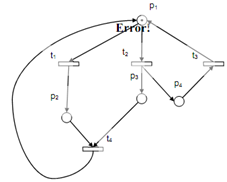
Figure: (a): An Unbounded Deadlock-able Non-Resolvable Net System
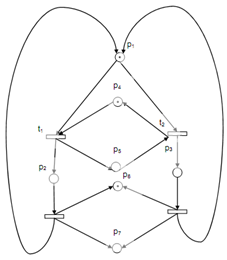
Figure: (b): Increasing the Number of Initial Markings 'Kills', the Live Net System
We can clearly consider that firing of transition t2 providing us a new marking M(0, 0, 1, 1) that means that p3 and p4 acquire one tokens each. Here by firing t2 we acquire a new marking M1 (1, 0, 1, 0). While we iterate this step n times the marking Mn(1, 0, n, 1) is attained. Hence we can consider that marking of p is dependent on the number of times we flow the tokens whereas firing the transitions t2 and t4. If we arbitrarily raise number of iterations to a very huge value then a condition termed as overflow can appear in these cases and the place p3 is said to be unbounded.
These situations should be carefully dealt along with as unbounded-ness is a pathological or unwanted situation. In other words we must say that the property of bounded-ness is a more advantageous situation.
In the similar manner Petri net if we fire transition t1 then it is clearly observable that no other transition able to be fired and the system come into a state of deadlock. It is a extremely not wanted situation. This is desirable for each model to be in a deadlock-free state and hence at least one transition must always convince the conditions for firing.
Once again we have a state of liveliness that is stronger than deadlock-freeness. A transition is live whether it is potentially friable in all reachable markings. Hence a live transition all the time has the possibility of firing and a net system is termed as live if all the transitions are friable.
The reversibility's property holds a significant position in the Petri net modelling analysis. A reversible net system is only that can reach to its initial marking from any of its intermediate markings. In the following figure (a), the above situation is not satisfied and so lead to a nonreversible net structure. If a total deadlock is attained at any reachable marking, the net system can't be reversible except the reverse is not all times true. Therefore a system might not be reversible however; it can hold the liveliness and thus deadlock-freeness.