Cyrus Beck Algorithm - Line Clipping Algorithm

Cyrus Beck Line clipping algorithm is actually, a parametric line-clipping algorithm. The term parametric means that we require finding the value of the parameter t in the parametric representation of the line segment for the point at that the segment intersects the clipping edge. For good understanding, identify the Figure (a) as in above, here P Q is a line segment, that is intersecting at the two edges of the convex window.

Note: The algorithm is appropriate to the "convex polygonal window".

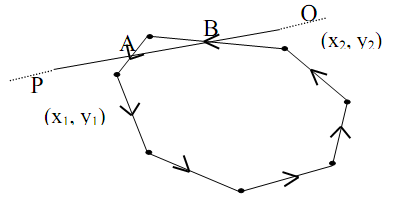
Figure: (a): Interaction of line PQ and Window

Here, just again call the parametric equation of line segment PQ that we have already studied.

This is simply    P + t (Q - P)      0 ≤ t ≤ 1

Here, t → linear parameter incessantly changes value.

∴P + t (Q - P) ⇒ (x₁, y₁) + t (x₂ - x₁, y₂ - y₁) = (x, y) be any point on PQ.    ------ (1)

For such equation (1) we have subsequent cases:

1)   While t = 0 we obtain the point P.

2)   While t = 1 we get the point Q.

3)   While t varies then 0 ≤ t ≤ 1 then line in between point P and Q is traced.

 For t = ½ we find the mid-point of PQ.

4)   While t < 0 line on Left hand side of P is traced.

5)   While t > 1 line on Right hand side of Q is traced.

Consequently, the variation in parameter t   is actually generating line in point wise method. The range of the parameter values will discover the portion to be clipped through any of convex polygonal region consisting of n-vertices or lattice points to be identified through the user. There is one type of clipping situation is shown in Figure (a) of Interaction of line PQ and Window.