Cross Product

In this last section we will look at the cross product of two vectors.  We must note that the cross product needs both of the vectors to be three dimensional (3D) vectors.  

 As well, before getting into how to calculate these we should point out a major variation in between dot products and cross products. The product of a dot product is a number and the result of a cross product is a vector!  Be cautious not to confuse the two.

Thus, let's begin with the two vectors a^→ = (a₁, a₂, a₃) illustrated by the formula, and b^→ = (b₁, b₂ , b₃) then the cross product is illustrated by formula

a^→ * b^→ = (a₂b₃ - a₃b₂, a₃b₁ - a₁b₃, a₁b₂ - a₂b₁)

This is not a simple formula to remember.  There are two methods to derive this formula.  Both of them make use of the fact that the cross product is actually the determinant of a 3x3 matrix.  If you don't be familiar with what this is that is don't worry about it.  You don't require to know anything about matrices or determinants to make use of either of the methods.  The notation for the determinant is like this,

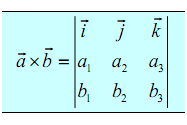
The first row in the above determinant is the standard basis vectors and should appear in the order given here.  The 2^nd row is the components of a? and the third row is the components of b^→.  Now, let's take a look at the dissimilar methods for getting the formula.

 The first technique uses the Method of Cofactors.  If you do not know the method or technique of cofactors that is fine, the result is all that we want.  Formula is given below:

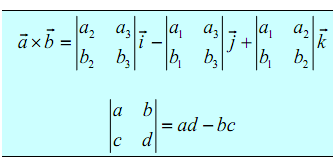
This formula is not as hard to remember as it might at first come out to be.  First, the terms change in sign and notice that the 2x2 is missing the column below the standard basis vector that multiplies it also the row of standard basis vectors.

The second method is little easier; though, many textbooks don't cover this method as it will only work on 3x3 determinants.  This technique says to take the determinant as listed above and after that copy the first two columns onto the end as displayed below.

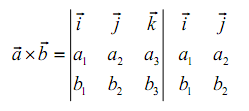
We now have three diagonals which move from left to right and three diagonals which move from right to left.  We multiply all along each diagonal and add those that move from left to right and subtract those which move from right to left.