We can compute any forward rate using the spot rate. When we tell 3 years forward rate 4 years from now, there are two elements to consider. One is the length of the time for the rate, i.e., 3 years in our example and the second element is when in future the rate begins, and in our example it is 4 years. The notation used to represent the forward rate is _l f_n.

There are two subscripts in the notation. Subscript 'l' refers to the length of time in which the rate applies and the subscript 'n' refers to when the forward rate begins. 

Suppose an investor wants to invest Rs.100, and his investment horizon is l + n period.  The two options available to the investor are: purchase a zero-coupon bond with a maturity period of l + n or alternatively, purchase a zero-coupon bond with a maturity of l period and then reinvest the proceeds on maturity in a zero-coupon bond for n period. The investor will be indifferent towards the two alternatives if they produce the same return over the l + n investment horizon.

In the first option, the proceeds for this investment at the horizon date assuming that the semiannual rate is y _l+n, will be

         $100 (1+ y_l+n)^l+n

For the second option, assuming that the semiannual rate is y_m, the proceeds at the end of m periods will be,

         $100 (1+ y_m)^m

When the proceeds are received in m periods, they are reinvestment at the forward rate,  _t f_m, producing a value for the investment at the end of m + t periods of

         $100 (1+ y_m) ^m (1+ _t f_m)^t

The investor would be indifferent to the two alternatives when,

         $100 (1+ y_m+t)^m+t = Rs.100 (1+ y_m) ^m (1+ _t f_m)^t

Solving it for _t f_m,

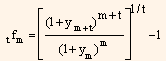
If t is equal to 1, the formula reduces to the 1 period (6-month) forward rate.