From past experience a machine is termed to be set up correctly on 90 percent of occasions.  If the machine is set up correctly then 95 percent of good parts are expected however if the machine is not set up correctly then the probability of a good part is only 30 percent.

On a specific day the machine is set up and the first component produced and found to be good.  What is the probability that the machine is set up appropriately.

Solution:

This is shown in the form of a probability tree or diagram as given below:

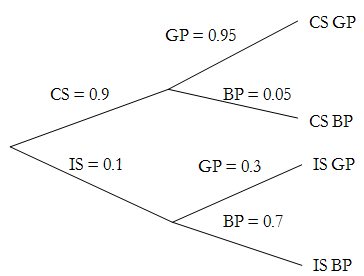
 Whereas: CS - Correct Setting

IS - Incorrect Setting

GP - Good Product

BP - Bad Product

P(CSGP) = 0.9 × 0.95 = 0.855

P(CSBP) = 0.9 × 0.05 = 0.045

P(ISGP) = 0.1 × 0.3 =   0.03

P(ISBP) = 0.1 × 0.7 =    0.07

                                   1.00

- Probability of obtaining a good part (GP) = CSGP or ISGP

                                                            = CSGP + ISGP

                                                            = 0.855 + 0.03 = 0.885

Note: Good parts may be produced while the machine is correctly set up and when also it's incorrectly setup. In 1000 trials, 855 occasions while its correctly setup and good parts produced as CSGP and 30 occasions while its incorrectly setup and good parts produced as ISGP.

- Probability that the machine is correctly set up after getting a good part.

= number of favoural outcomes/total possible outcomes

=P (CSGP)/P(GP)

= 0.855/ 0.885

= 0.966

Or

= P (CS|GP)

= P (CSGP)/P(GP)

= 0.855/ 0.885

= 0.966