Computation of a DFA or NFA without ε-transitions
An ID (q1,w1) computes (qn,wn) in A = (Q,Σ, T, q0, F) (in zero or more steps)
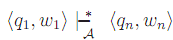
if there is a sequence of IDs (q1,w1), . . . qn,wn)) in which, for all i > 1, 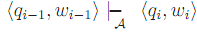
A computation of an FSA A on input w is a computation from the initial ID (q0,w) to a terminal ID: ((q0,wi, . . . , (q, ε)).
The fact that |-A is no longer partial functional implies that we can no longer speak of the computation of A on hq1,w1i. What's more, while every computation is ?nite, it is no longer true that they all take exactly |w1| steps. Computations end when they reach an ID with no successor; this can now be either because the entire input was scanned or because an ID hq, σ � wi was reached for which δ(q, σ) = ∅. Only the ?rst case represents successful processing of w1 by A; we need to be careful to distinguish "halting" computations from those that "crash".