Calculate the whole reaction at block:

A bar weighing 1 kg/m is bent at right angles into segments 0.60 m and 0.30 m long. It takes the position illustrated in Figure, while the frame F to which this is pinned at A is accelerated horizontally. Calculate this acceleration and the whole reaction at A.

Solution

Figure shows the free body diagram in which all of the forces acting on the body are illustrated. We must understand that inertia forces acting upon the bar only shall keep it in the shown position. Figure (c) illustrated the distances of several forces in equilibrium position.

From FBD, we may write the following equilibrium equations,

∑ F_x  = 0, X _A  = 0.6 a + 0.3 a

∑ F_y  = 0, Y_A  = 0.6 g + 0.3 g

= 8.83 N

Algebraic sum of the moment of all of forces about point A, i.e. ∑ M _A  = 0

∑ M _A  = 0,   0.6 a × 27.70 + 0.3 a × 61.2 - 0.6 g ×11.5 - 0.3 g × 13.84 = 0

       ∴ 16.62 a + 18.36 a - 11.055 g = 0

            ∴ a = 3.10 m / sec ²

         ∴ X _A  = 0.9 × 3.10 = 2.80 N

∴ Total resultant reaction at A =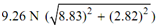, and

tan θ =( 8.83 /2.80) = 3.16

θ= 72.41^o