Calculate the maximum and minimum stress:

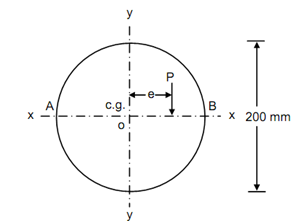
A cast iron column of 200 mm diameter carries a vertical load of 400 kN, at a distance of 50 mm from the centre. Calculate the maximum & minimum stress developed in the section, along with the diameter passing through the point of loading.

(a)

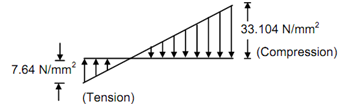
(b) Stress Distribution along the Diagonal

Figure

Solution

Vertical load, P = 400 kN = 400 × 10³ N

Diameter of the section, D = 200 mm

Area of the section,  A = (π/4) (200)²  = 31416 mm²

Direct stress, f₀ =(P/A) =4 × 10⁵/31416 = 12.732 N/mm2

Eccentricity, e = 40 mm

Bending moment, M = P × e = (400 × 10³ ) 40 = 16 × 10⁶  N-mm

Section modulus, z = π D ³/32            = π (200)³ /32= 785.4 × 10³ mm³

Bending stress,  f =± Pe / Z =±  16 × 10⁶ /785.4 × 10³=± 20.372 N/mm2

 ∴ Resultant stress at the edge, B = f₀  + f_b  = 12.732 - 20.372

                                                     = 33.104 N/mm² (compressive)

∴ Resultant stress at the edge, A =  f₀  - f_b  = 12.732 - 20.372

                                                        =- 7.640 N/mm² (tensile)

The stress distribution along with the diameter is as illustrated in Figure (b).