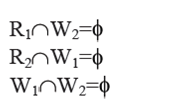Bernstein Conditions for Detection of Parallelism
For implementation of instructions or block of instructions in parallel, it should be guaranteed that the instructions are independent of each other. These instructions can be / control dependent / data dependent resource dependent on each other. We are considering only data dependency between the statements for taking decisions of parallel implementation. A.J. Bernstein has implicated the work of data dependency and resultant some conditions based on which we can settle on the parallelism of processes or instructions.
Bernstein conditions are rely on the subsequent two sets of variables:
i) The input set or Read set RI that consists of memory locations examine by the statement of instruction I1.
ii) The output set or Write set WI that consists of memory locations printed into by instruction I1.
The sets WI and RI are not disjoint as the similar locations are used for writing and reading by SI.
The following are Bernstein Parallelism conditions which are determine to conclude whether the statements are parallel or not:
1) Position in R1 from which S1 reads and the Position W2 onto which S2 writes must be commonly exclusive. It means S1does'nt read from any memory location onto which S2 writes. It can be indicated as:
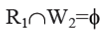
2) Likewise, locations in R2 from which S1 writes and the locations W1 onto which S2 reads must be commonly exclusive.It means S2 does not read from some memory location onto which S1 writes. It can be indicate as:
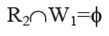
3) The memory locations W1 and W2 onto which S1 and S2 write, should not be examine by S1 and S2. It means R1 and R2 should be free of W1 and W2. It can be indicated as :
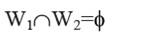
To demonstrate the operation of Bernstein's conditions, let consider the following instructions of sequential program:
I1 : x = (a + b) / (a * b)
I2 : y = (b + c) * d
I3 : z = x2 + (a * e)
Now, the read set and write set of I1, I2 and I3 are as given:
R1 = {a,b} W1 = {x}
R2 = {b,c,d} W2 = {y}
R3 = {x,a,e} W3 = {z}
Now let us search out whether I1 and I2 are parallel or not