Solve discrete harmonic mapping of a given surface patch (suppose the surface is genus-0 and with one boundary)

1. Map the boundary loop onto a unit rectangle using chord-length parameterization:

a) Pick a random starting point B0, trace the boundary loop L, compute its total length |L|;

b) Starting from B0, find vertices B1, B2, B3 on L, such that the lengths of the boundary paths from B0 to B1, B2, and B3 , are (or just passed) |L|/4, |L|/2, and 3|L|/4, respectively;

c) Map B0, B1, B2, and B3, to (0,0), (1,0), (1,1), and (0,1) respectively, map curve segments (B0, B1), (B1, B2), (B2, B3), (B3, B0) to four boundaries of the unit square accordingly using chord-length parameterization. This fixes the boundary mapping: all boundary vertices are mapped.

2. For every interior vertex, map it to the weighted average center of its one-rings. The weight is the harmonic weight, i.e., the cotangent weight defined on the original mesh.

Initially, map all interior vertices to (0.5,0.5), then use one of the following two ways to find the solution:

A easier but slower way:

Iteratively move the mapping position of each vertex:

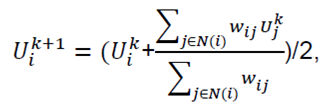
Here u denotes the coordinates on the plane, and we use k and k+1 to indicate the position before and after the (k+1)-th iteration.

* You may need to do a few thousand iterations until you see the movement is small.

A faster way:

Assemble the coefficient matrix and solve the linear system (check slides)