Find out the volume of the solid obtained by rotating the region bounded by y = x² - 2x and  y = x about the line y = 4 .

Solution: Firstly let's get the bounding region & the solid graphed.

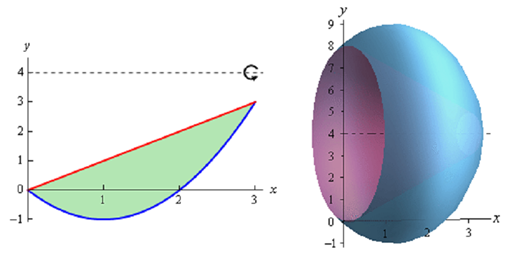
Again, we will be looking for the volume of the walls of this object. Also since we are rotating around a horizontal axis we know that the cross-sectional area will be a function of x.

Given are a couple of sketches of the boundaries of the walls of this object in addition to a typical ring. The sketch on the left involved the back portion of the object to specify a little context to the figure on the right.

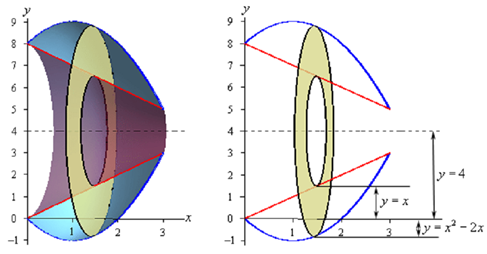
Now, we have to be careful here in finding out the inner & outer radius. Let's begin with the inner radius as this one is little clearer.  Firstly, the inner radius is not x. The distance from x-axis to the inner edge of the ring is x, however we desire the radius and i.e. the distance from the axis of rotation to the inner edge of the ring.  Therefore, we know that the distance from the axis of rotation to the x-axis is 4 & the distance from the x-axis to the inner ring is x. The inner radius have to be then be the difference among these two.  Or,

                                   inner radius = 4 - x

The outer radius works the similar way.  The outer radius is,

outer radius = 4 - ( x² - 2 x ) = - x² + 2 x + 4

 Note as well that given the location of the typical ring in the sketch above the formula for the outer radius might not look quite right however it is actually correct.  As sketched the outer edge of the ring is below the x-axis & at this point the value of the function will be negative and therefore when we do the subtraction in the formula for the outer radius we'll in fact be subtracting off a negative number that has the net effect of adding this distance onto 4 and which gives the correct outer radius. Similarly, if the outer edge is above x-axis, the function value will be positive and therefore we'll be doing an honest subtraction here and again we'll get the accurate radius in this case.

The cross-sectional area for this case is following,

A ( x ) = ∏ ((- x² + 2x + 4)²  - ( 4 - x )² ) = ∏ ( x⁴ - 4 x³ - 5x² + 24 x )

The first ring will take place at x =0 and the last ring will take place at x = 3 and therefore these are our limits of integration. The volume is then,

V = ∫_a^b A(x)dx

  = ∏∫ ³₀  x⁴ - 4x³  - 5x² + 24x dx

   = ∏  (1/5 x⁵ - x⁴ - 5/3 x³ + 12x² )|³₀

     = 153 ∏ /5