Arc Length with Vector Functions

In this part we will recast an old formula into terms of vector functions.  We wish to find out the length of a vector function,

r^→ (t) = {f (t), g(t) , h (t)}

on the interval a ≤ t ≤ b .

in fact we already know how to do this.  Remind that we can write the vector function into the parametric form,

 x = f (t)

 y = g(t)

z = h (t)

As well, remind that with two dimensional parametric curves the arc length is illustrated by,

L = ∫^b_a √ [f' (t)]² + [g' (t)]² dt

Here is a natural extension of this to three dimensions. Thus, the length of the curve r ?t ? on the interval a ≤ t ≤ b is,

L = ∫^b_a √ [f' (t)]² + [g' (t)]² + [h' (t)] dt

There is a good simplification which we can make for this.

Note: The integrand that is the function we're integrating is nothing much more than the magnitude of the tangent vector,

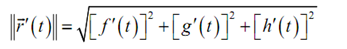
 Hence, the arc length can be written as,

L = ∫^b_a || ^→r' (t)|| dt