Add a Multiple of a Row to Another Row. In the operation we will replace row i with the addition of row i & a constant, c, times row j. The notation we'll utilize for this operation is Ri + cR j → Ri . To carry out this operation we will take an entry from row i & add to it c times the corresponding entry from row j & put the result back into row i. Following is an example of this operation.
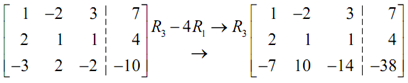
Let's do the individual computation to ensure you followed this.
-3 - 4 (1) = -7
2 - 4 ( -2) = 10
-2 - 4 (3)= -14
-10 - 4 (7 ) = -38
Be careful with signs here. We will be doing these computations with our head for the most of the part and it is very simple to mix up signs and adds one in that doesn't belong or lose one that must be there.
It is extremely important which you can do this operation as this operation is the one that we will be using more than the other two combined.
So how do we utilize augmented matrices & row operations to solve systems? Let's begin with a system of two equations & two unknowns.
ax + by = p
cx + dy = q
First we write down the augmented matrix for this system,
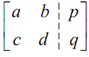
and utilizes elementary row operations to convert it into the given augmented matrix.
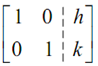
Once we contain the augmented matrix in this form we are done. The solution to the system will be x = h and y = k.
Example 1 Solve out following systems of equations.
3x - 2 y = 14
x + 3 y = 1
Here the primary step is to write down the augmented matrix for this system.
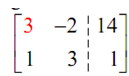
To convert it in the final form we will begin in the upper left corner & the work in a counter- clockwise direction till the first two columns seem as they must be.
Thus, the first step is to make the red three in the augmented matrix above in a 1. We can utilize any of the row operations which we'd like to. However, we must always try to minimize the work as much as possible.
Thus, as there is a one in the first column already only it isn't in the correct row let's utilizes the first row operation & interchange the two rows.
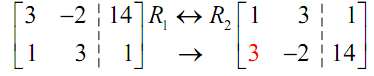
The next step is to obtain a zero below the 1 that we just got in the upper left hand corner. It means that we have to change the red three into a zero. It will almost always need us to utilize third row operation. If we add -3 times row 1 onto row 2 we can convert that 3 in a 0. Following is that operation.
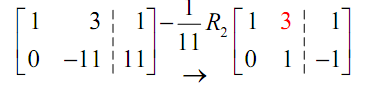
Next we have to get a 1 into the lower right corner of the first two columns. It means varing the red -11 into a 1. Usually this is accomplished with the second row operation. If we divide the second row by -11 . We will obtain the 1 in that spot which we need.
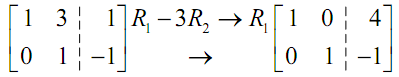
The last step is to turn the red three into a zero. Again, it almost always needs the third row operation. Following is the operation for this final step.
We have the augmented matrix in the needed form and hence we're done. The solution to this system is x = 4 and y = -1.
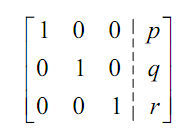
This is significant to note that the path we took to get the augmented matrices in this instance into the final form is not the only path that we could have utilized. There are several different paths that we could have gone down. Every path would have arrived at the same last augmented matrix though so we have to always choose the path that we feel is the simplest path. Note that different people may feel that different paths are simpler and hence may well solve the systems differently. They will get the similar solution however.
For two equations & two unknowns this procedure is probably a little more complex than just the straight forward solution procedure we utilized in the first section of this chapter. This procedure does start becoming useful while we start looking at larger systems. Thus, let's take a look at a couple of systems along with three equations in them.
In this case basically the procedure is alike except that there's going to be more to do. As along with two equations we will primary set up the augmented matrix and then utilizes row operations to put it into the form,
Once the augmented matrix is in this form the solution is x = p , y = q and z = r . As with the two equations case there actually isn't any fix path to take in getting the augmented matrix into this form. The usual path is to get the 1's in the accurate places and 0's below them. Once it is done then we try to get zeroes above the 1's.