Reference no: EM13342956
1. A triangle in a graph is defined as a triple of vertices (u, v, w) in which (u, v), (v, w) and (u, w) are edges in the graph. Answer the following questions and provide your best justification.
a. What is the number of triangles in a complete graph with vertices?
b. What is the expected number of triangles in an Erdos-Rényi graph , a graph on vertices where each edge appears with a probability independently?
2. The friendship paradox is the phenomenon that most people have fewer friends than their friends have, on average. This question asks for a mathematical explanation of the phenomenon. Given an undirected graph , where the set of vertices corresponds to the people in the social network, and the set of edges corresponds to the friendship relation between pairs of people. Denote by the degree of vertex .
We can compute the following quantities.
+ The average number of friends of a (random) person in the graph:
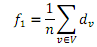
+ The average number of friends that a typical friend has can be computed as follows.
Choose, uniformly at random, an edge of the graph and an edge of the graph and an end point of that edge, and calculate the degree of the selected end point. That is
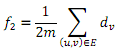
a) Prove that and provide your best justification.
3. Write a program in your preferred programming language to compute edge betweeness centrality of edges in an undirected graph. The program will read the graph from a file called "graph.txt" and output the edge degree centrality of edges to a file called "edge_betweeness.txt".
The file "graph.txt" includes multiples lines in which the first line contains two integers and that correspond to the number of nodes and edges in the graph. Each of the following lines contain two integers and , separated by one space, to denote an edge from to . Nodes are numbered from to .
The output file "edge_betweeness.txt" contains exactly m lines in which the line is the edge betweeness of the th edge in the input file.
Your submission must include
- The source file(s)
- The sample input/output
- A README file that describes the compile and running instruction
4. Visualize your own Facebook network following the Gephi tutorial in the class.
a. Report top 3 people in your networks according to their degree, betweeness centrality, and eigenvector centrality.
b. Export the final network to a PDF file lastname_firstname.pdf and upload the file to Blackboard.
Attachment:- degree.rar
|
What is the final volume of the gas
: 0.17 mol of argon gas is admitted to an evacuated 54.83 cm3 container at 27°C. What is the final volume of the gas
|
|
How the internet-intranet-e-commerce will be integrated
: Describe how the Internet/intranet/e-commerce will be integrated into the business, as well as the benefits that these technologies would bring to the business.
|
|
Explain how much mercury will remain after 7 days
: The half-life of mercury-197 is 64.1 hours. A. If a patient undergoing a kidney scan is given 5.0 ng of mercury-197, how much will remain after 7 days? B. After 33 days
|
|
Estimate the angular acceleration of the disk
: A 4-kg block lies on a horizontal table whose coefficient of friction is 0.3. A horizontal rope is redirected by a uniform solid disk (pulley) of mass 2 kg to a mass of 12-kg hanging off the table. What is the angular acceleration of the disk
|
|
What is the number of triangles in a complete graph
: What is the number of triangles in a complete graph with vertices and what is the expected number of triangles in an Erdos-Rényi graph , a graph on vertices where each edge appears with a probability independently?
|
|
How many milliliters must be administered intravenously
: A solution of selenium-75, a radioisotope used in the diagnosis of pancreatic disease, is found just prior to administration to have an activity of 44 uCi/mL. How many milliliters should be administered intravenously for a dose of 175 uCi
|
|
Determine the standard cost per dress for direct materials
: Determine (a) the standard cost per dress for direct materials and ,direct labor; (b) the priceVariance, quantit ariance, and total direct matd4als cost variance; and (c) the rate \ypi, fiance, time' v, lance, and total dire,Sbor cost variance.
|
|
What is the output function of the filter
: If you input the function x[n]=0,1,0,1,0,1,0,1,0,1 into a digital filter with impulse response h[m]=1,0,1, what is the output function y[n] of the filter
|
|
Explain the oxidation number of mn before reaction
: What is the oxidation number of Mn before and after the reaction- 5H2AsO3 + 2MnO4- + 6H+ + 2Mn2+ + 5H3AsO4 + 3H2O
|