Reference no: EM131016672

Question:

1. A router has the following entries in its routing table:

Address/Mask                          Next hop

135.46.56.0/22                        Interface 0

135.46.60.0/22                        Interface 1

192.53.40.0/23                        Router 1

default                                   Router 2

For each of the following IP addresses, what does the router do if a packet with that address arrives?

(a) 135.46.63.10
(b) 135.46.57.14
(c) 135.46.52.2
(d) 192.53.40.7
(e) 192.53.41.7

2. Questions related to IP addressing:

(1) A network on the Internet has a subnet mask of 255.255.240.0. What is the maximum number of hosts it can handle?

(2) Suppose an ISP owns the block of addresses of the form 101.101.128.0/17. Suppose it wants to create four subnets from this block, with each block having the same number of IP addresses. What are the prefixes (of form a.b.c.d/x) for the four subnets.

3. Questions related to IP fragmentation and reassembly:

(1) Consider IP datagram as illustrated in Figure 6 of RFC 791, except that the total length field is 1200. If this datagram were to traverse a local network that had a maximum transmission unit size of 500 bytes it would have to be fragmented. Assume it is fragmented into three smaller datagrams according to the algorithm presented Section 3.2 (see subsection titled ``An Example Fragmentation Procedure'') of RFC 791. With this technique, each fragment (except the last) is made the maximum allowable size. What are the values of the header length, total length, identification, flags, and fragment offset fields for all three fragment headers?

(2) Assume that the datagram fragments from the previous problem finally reach the destination host which has to reassemble them into a single datagram before passing them "up" to the TCP module. How does the IP module on the destination host know which fragments belong to the original IP datagram and how long it is (Hint: the "more fragments" bit plays a role in this)?

4. Consider the following network example. With the indicated link costs along each link in the figure, use Dijkstra's shortest-path algorithm to compute the shortest path from x to all network nodes. Show how the algorithm works by computing a table.

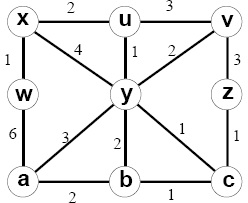
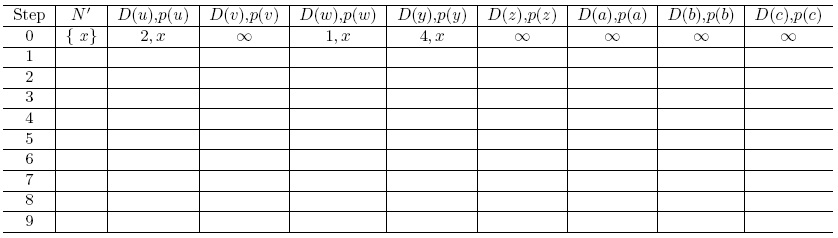
Answer: Let N' denote the set of nodes whose distance have been known so far, D(s) be the distance to a node s, and p(s) be the parent node of the node s on the shortest path from s to node x. We then construct the following table.

5. Consider the following network example. Suppose that the distance vector (DV) routing algorithm is used to compute the distance between nodes.

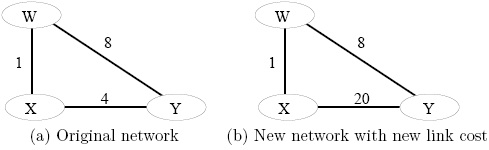
(a) Show the procedure of nodes X, Y and W computes their Distance Vector for network illustrated by Figure (a), i.e., link costs are C(xw)=1, C(xy)=4, and C(yw)=8.

Answer: In the following, each column shows the node X, Y and Z's table update respectively:

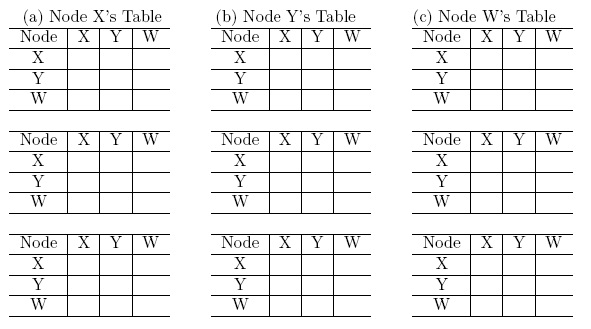
(b) Assume that after the DV is computed by all nodes, the link cost of xy changed from 4 to 20. Show the procedure of nodes X, Y and W updates their Distance Vector for network illustrated by Figure (b), i.e., link costs are C(xw)=1, C(xy)=20, and C(yw)=8.

Answer: In the following, each column shows the node X, Y and Z's table update respectively:

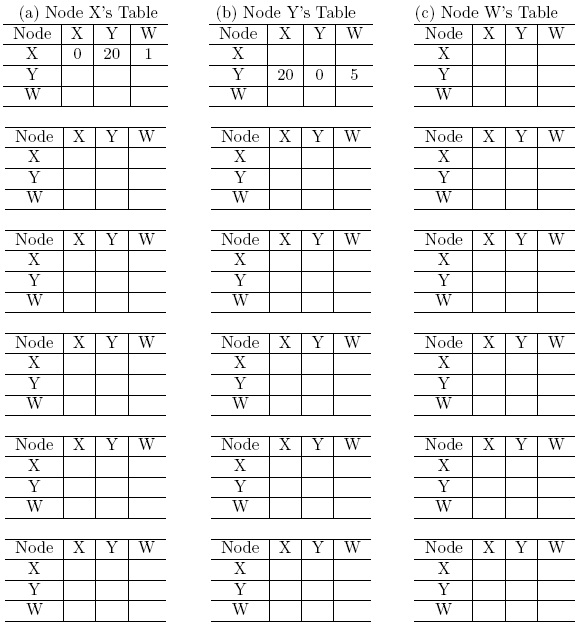
* If not enough, add more tables by yourself

6. We studied Dijkstra's link-state routing algorithm for computing the unicast paths that are individually the shortest paths from the source to all destinations. The union of these paths might be thought of as forming a shortest path tree. If each links has an associated cost and the cost of a tree is the sum of the link costs, then a spanning tree whose cost is the minimum of all of the spanning trees is called a minimum spanning tree. Both shortest path tree and minimum-spanning tree can be used for broadcast routing. By constructing a counterexample, show that the least-cost path tree is not always the same as a minimum spanning tree.

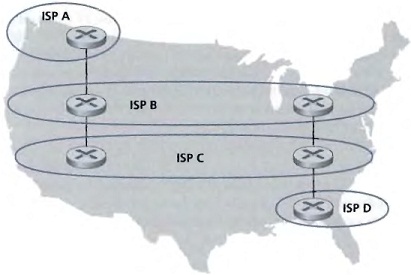
7. Consider the following network. ISP B provides national backbone service to regional ISP A. ISP C provides national backbone service to regional ISP D. Each ISP consists of one AS. B and C peer with each other in two places using BGP. Consider traffic going from A to D. B would prefer to hand that traffic over to C on the West Coast (so that C would have to absorb the cost of carrying the traffic cross-country), while C would prefer to get the traffic via its East Coast peering point with B (so that B would have carried the traffic across the country). What BGP mechanism might C use, so that B would hand over A-to-D traffic at its East Coast peering point? To answer this question, you will need to dig into the BGP specification.