Utilizes the definition of the limit to prove the given limit.

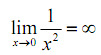
Solution

Let M > 0 be any number and we'll have to choose a δ > 0 so that,

1/ x²  > M                                                  whenever   0 < |x - 0 | <|x|< δ

We'll begin with the left inequality and attempt to get something in the end which looks like the right inequality.  To do this basically we'll solve the left inequality for x and we'll need to recall that √x²  = |x| .  Hence, here's that work.

1/x²  > M ⇒     x²  <  1/M ⇒    |x| <     1/√M

Thus, it looks like we can select δ =1/√M       .  All we have to do now is verify this guess.

Let M > 0 be any number, select δ =1/√M and suppose that 0 < |x| <1/√M   .

We tried to illustrate that our supposition satisfied the left inequality through working with it directly.  Though, in this, the function and our supposition on x that we've got in fact will make this easier to begin with the supposition on x and illustrates that we can get the left inequality out of that.  Note as well that this is being done this way mostly due to the function that we're working along with and not due to the type of limit that we've got.

Doing this we get ,

|x| <     1/√M              

|x| ²<    1/M                                                  square both sides

x²  <     1/M                                               acknowledge that |x| ² 2

1/x² >M                                                   solve for x²

Thus, we've managed to illustrate that,

1/ x² > M                   whenever           0 < |x - 0 | < 1/√M              

and thus by the definition of the limit we have,

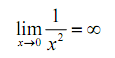
For our following set of limit definitions let's look at the two definitions for limits at infinity. Again, we require one for a limit at plus infinity & another for negative infinity.