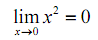Utilizes the definition of the limit to prove the given limit.

Solution

In this case both L & a are zero.  So, let ε < 0 is any number.  Don't worry regarding what the number is, ε is only some arbitrary number.   Now in according to the definition of the limit, if this limit is to be true we will have to determine some other number δ > 0 so that the following will be true.

|x² - 0| < ε               whenever             0< |x-0|< δ

Or upon simplifying things we required,

                |x²   |< ε                whenever            0<|x|<0

Often the way to go through these is to begin with the left inequality & do a little simplification and distinguish if that recommend a choice for δ .  We'll begin by bringing the exponent out of the absolute value bars & then taking the square root of both sides.

                                |x|²   < ε   ⇒  |x| <√ ε

Now, the results of this simplification looks an awful lot like 0 <|x|< ε  along with the exception of the " 0 < " part. Missing that though isn't a problem; this is just telling us that we can't take x = 0 .  Thus, it looks like if we choose δ =√ ε .we have to get what we want.

We'll next have to verify that our choice of δ will give us what we desire, i.e.,

  |x|²   < ε         ⇒  0< |x| <√ ε

Verification is actually pretty much the similar work that we did to get our guess.  Firstly, let's again let ε < 0 be any number and then select δ =√ ε.  Now, suppose that 0 <| x | <√ ε.  We have to illustrates that by selecting x to satisfy this we will obtain,

                                                    |x²|   < ε

To begin the verification process we'll start with | x²| and then first strip out the exponent from the absolute values. Once it is done we'll employ our assumption on x, namely that  |x| < ε. Doing ball this gives,

|x²|   =|x| ²           strip exponent out of absolute value bars

      < (√ ε)²        use the assumption that    |x|   < ε

        = ε            simplify

Or, upon taking the middle terms out, if we suppose that 0 < |x |<√ ε .then we will get,

                                          |x²|   < ε

and this is accurately what we required to show.

Thus, just what have we done?  We've illustrated that if we choose ε >0 then we can determine a δ> 0  so that we have,

                                                         |x² - 0 |< ε

and according to our definition it means that,