The Mean Value Theorem for Integrals

If f(x) is a continuous function on [a,b] then here is a number c in [a,b] thus,

_a∫^b f(x) dx = f(c)(b -a)

Proof

Let's begin off by defining,

F(x) = _a∫^b f(t) dt

Because f(x) is continuous we get alreday from the Fundamental Theorem of Calculus, Part I that F(x) is continuous on [a,b], differentiable on (a,b) and as F′(x) = f(x).

Here, from the Mean Value Theorem we get that here is a number c such as a < c < b and that,

 F(b)- F(a) = F′(c) (b - a)

Though we know that F′(c) = f(c) and,

 F(b) = _a∫^b f(t) dt = _a∫^b f(x) dx                           F(a) = _a∫^a f(t) dt = 0

Therefore we get,

_a∫^b f(x) dx = f(c) (b -a)

Work

The work done by the force F(x) as by assuming that F(x) is continuous, over the range a ≤ x ≤ b is,

W = _a∫^b F(x) dx

Proof

Let's begin off by dividing the range a ≤ x ≤ b in n subintervals of width ?x and from all of these intervals select the points x₁*, x₂*,...., x_n*.

Here, if n is large and as F(x) is continuous we can suppose that F(x) won't differ by much over each interval and therefore in the i^th interval we can suppose that the force is approximately constant along with a value of F(x) ≈ F(x*). The work on every interval is then approximately,

W_i ≈ F(x_i*) ?x

The complete work over a ≤ x ≤ b is approximately then,

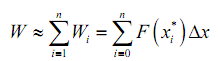
At last, if we take the limit of that as n goes to infinity we will find the exact work done. Therefore,

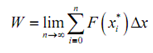
It is, though, nothing more than the definition of the definite integral and therefore the work done through the force F(x) over a ≤ x ≤ b is,

W = _a∫^b F(x) dx