Tangents with Parametric Equations

In this part we want to find out the tangent lines to the parametric equations given by

X= f (t)

Y = g (t)

To do this let's first remind how to find the tangent line to y = F(x) at x=a. now here the tangent line is illustrated by,

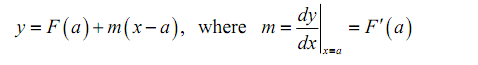
Now here, Note that if we could make out how to get the derivative dy/dx from the parametric equations we could just again use this formula as we will be capable to make use of the parametric equations to find out the x and y coordinates of the point.

Thus, just for a second let's assume that we were able to eliminate the parameter from the parametric form and write the parametric equations in the type y = F (x).

Now here, plug the parametric equations in for x and y. Yes, it look like silly to remove the parameter, after that immediately put it back in, but it's what we require to do to get our hands on the derivative. Doing this provides,

g (t) = F (f (t))  

Now, distinguish with respect to t and notice that we'll require to make use of the Chain Rule on the right hand side.

g' (t) = F' (f(t)) f' (t)

Let us do other change in notation.  We require to be careful along with our derivatives here. Lower case function's derivatives are regarding to t when derivatives of upper case functions are with respect to x.  Thus, to ensure that we keep this straight let's rewrite things like this.

dy/dt = F' (x) dx/dt

At this point we should recall ourselves just what we are after.  We required a formula for that is in words of the parametric formulas. 

Note: though that we can obtain that from the exceeding equation.

dy/dx = (dy/dt) / (dx/dt) ,         given dx/dt ≠ 0

Notice also that this will be a function of t and not x.