Systems of Equations Revisited

We require doing a quick revisit of systems of equations. Let's establish with a general system of equations.

a₁₁ x₁ + a₁₂ x₂ +................+a_1n x_n = b₁

a₂₁ x₁ + a₂₂ x₂ +.............. +a_2n x_n  = b₂

...................

a_n1 x₁ + a_n2 x₂ +............... +a_nn x_n  = b_n                              ...................(1)

Here, covert each side in a vector to find,

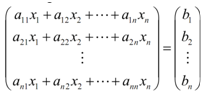
The left side of such equation can be thought of like a matrix multiplication.

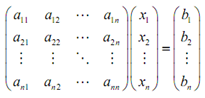
Simplifying up the notation a little provides,

A x? = b?   ................................(2)

Now there, x? is a vector that elements are the unknowns in the original system of equations.

We take (2) the matrix form of the system of equations (1) and resolving (2) is equal to solving

(1). the solving process is identical. The augmented matrix for (2) is,

A(b?)

Once we contain the augmented matrix we proceed as we did along with a system which hasn't been wrote in matrix form.

We also have the subsequent fact regarding to solutions to (2).

Fact

Provided the system of equation (2) we contain one of the subsequent three possibilities for solutions.

1.   There will be no more solutions.

2.   There will be particularly one solution.

3.   There will be infinitely various solutions.

Actually we can go a little farther here. Because we are assuming that we've got similar number of equations like unknowns the matrix A in (2) is a square matrix and therefore we can calculate its determinant. This provides the following fact.

Fact

Provided the system of equations in (2) we have the subsequent.

1.   If A is nonsingular then there will be particularly one solution to the system.

2.   If A is singular then there will either be no solution or infinitely various solutions to the system.

The matrix form of a homogeneous system is as,

A x?= 0?

 Here 0? is the vector of all zeroes. Under the homogeneous system we are guaranteed to have a solutions, x? = 0?. The fact above for homogeneous systems is so, Fact

Given the homogeneous system (3) we contain the subsequent.

1.   If A is nonsingular then the only solution will be x? = 0?

2.   If A is singular then there will be infinitely many nonzero solutions to the system.