The idea of this section is not to do anything new along with a series solution problem.  Instead this is here to exemplify that moving in a higher order differential equation does not actually change the process outside of making this a little longer.

Back into the Series Solution section we only looked at 2^nd order differential equations therefore we're going to do a quick illustration here involving a 3^rd order differential equation thus we can ensure and say that we've done at least one illustration with an order larger than 2.

Example1: Determine the series solution around x₀ = 0 for the following differential equation.

y''' + x² y' + xy = 0

Recall that we can only find a series solution about x₀ = 0 if that point is an ordinary point, or say as, if the coefficient of the highest derivative term is not zero on x₀  = 0.  It is clearly the case now thus let's start with the form of the solutions and also the derivatives which we'll require for this solution.

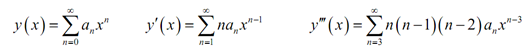
Plugging in the differential equation provides,

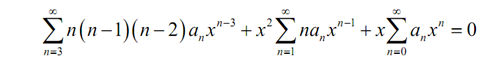
This time, move all the coefficients in the series and do suitable shifts hence all the series are in terms of xⁿ.

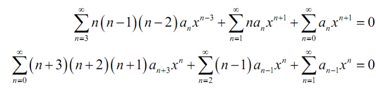
Subsequently, let's notice that we can create the second series at n = 1 as that term will be zero. Therefore let's do that and after that we can combine the second and third terms to find,

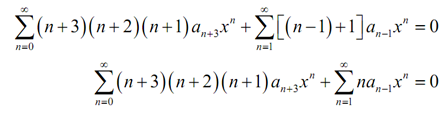
Therefore, we got a simple simplification into the new series that will assist with some additional simplification. The new second series can currently be started at n = 0 and after that combined with the first series to find,

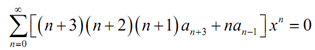
We can here set the coefficients equivalent to find a fairly simply recurrence relation.

(n + 3)(n + 2)(n + 1)a_n+3 + na_n-1 = 0,                 n = 0,1,2,...

Solving the recurrence relation provides,

a_n+3 = (-na_n-1)/((n +1) (n + 2) (n + 3)),                                      n = 0,1,2,...

Now we require starting plugging into values of n and it will be one of the major areas where we can notice a somewhat important increase in the amount of work needed when moving in a higher order differential equation.

n = 0: a₃ = 0

n = 1: a₄ = -a₀/(2x 3x 4)

n = 2: a₅ = -2a₁/(3x 4 x 5)

n = 3: a₆ = -3a₂/(4 x 5 x 6)

n = 4: a₇ = -4a₃/(5 x 6 x 7)

n = 5: a₈ = -5a₄/( 6 x 7 x 8) = 5 a₀/(2x 3x 4 x 5 x6 x 7 x 8)

n = 6: a₉ = -6a₅/( 7 x 8 x 9) = (2 x 6 x a₁)/(3x 4 x 5 x6 x 7 x 8 x 9)

n = 7: a₁₀ = -7a₆/(8 x 9 x 10) = (3 x 7 x a₂)/(4 x 5 x6 x 7 x 8 x 9 x 10)

n = 8: a₁₁ = -8a₇/(9 x 10 x 11) = 0

n = 9: a₁₂ = -9a₈/(10 x 11 x 12) = (-(5 x 9 x a₀))/(2 x 3 x 4 x 5 x6 x 7 x 8 x 9 x 10 x 11 x 12)

n = 10: a₁₃ = -10a₉/(11 x 12 x 13) = (-(2 x 6 x 10 x a₁))/(3 x 4 x 5 x6 x 7 x 8 x 9 x 10 x 11 x 12 x 13)

n = 11: a₁₄ = -11a₁₀/(12 x 13 x 14) = (-(3 x 7 x 11 x a₂))/(4 x 5 x6 x 7 x 8 x 9 x 10 x 11 x 12 x 13 x 14)

Okay, we can here break the coefficients down in 4 sub cases specified by a_4k, a_4k+1, a_4k+2 and a_4k+3  for k = 0,1, 2, 3,?  We'll give a semi-detailed derivation for a_4k and after that leave the remain to you with only couple of comments like they are nearly the same derivations.

First see that all the a_4k terms have a₀ in them and they will optional in sign. Next see that we can turn the denominator in a factorial, (4k!) to be exact, if we multiply top and bottom through the numbers which are already in the numerator and thus it will turn these numbers in squares.  Next see that the product in the top will create at 1 and rise by 4 till we reach 4k - 3.  Therefore, taking all of that in account we find,

a_4k = ((-1)^k (1)²(5)².....(4k -3)²a₀)/(4k)!

Here k = 1,2,3...

And see that this will only work starting along with k = 1 as we won't find a₀ out of this formula as we must by plugging in k = 0.

Here, for a_{4k +1} the derivation is almost same and hence the formula is,

a_4k+1 = ((-1)^k (2)²(6)².....(4k -2)²a₁)/(4k + 1)!

Here k = 1,2,3...

and again see that this was not work for k = 0

The formula for a_4k+2 is again nearly same except for this one see that we also require to multiply top and bottom with a² in order to find the factorial to seem in the denominator and thus the formula here is,

a_4k+2 = (2(-1)^k (3)²(7)².....(4k -2)²a₂)/(4k + 2)!

Here k = 1,2,3...

Noticing even one more time that it won't work for k = 0. At last, we have a_{4k +3} = 0 for k = 0,1, 2, 3,...

Now that we contain all the coefficients let's find the solution,

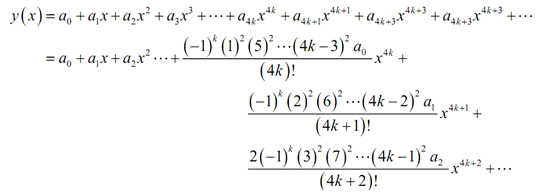
Collecting up the terms which contain identical coefficient (excluding for the first one in each case as the formula won't work for such) and writing all things as a set of series provides us our solution,

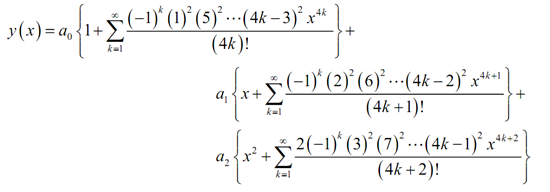
Therefore, there we have this. As we can notice the work in finding formulas for the coefficients was a bit messy since we had three formulas to find, but individually they were not as bad as even several of them could be when dealing with 2^nd order differential equations. Also note that while we found lucky with such problem and we were capable to find general formulas for the terms the higher the order the less likely this will turn into.