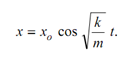Motion of this particle:
A particle of mass m is resting on a smooth horizontal plane as illustrated in Figure (a). It is associated to a spring which has a constant of k in force units per unit deformation. The mass is displaced to a distance xo from its equilibrium position and released with zero velocity. Learn the motion of this particle.
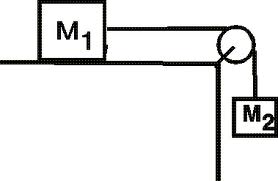
Solution
A free-body diagram is drawn showing the particle in a position at a distance x from equilibrium position. Referring Figure (b). A force T is acting on this body in a horizontal direction which is developed due to the stretching of the spring through the distance x.
Within elastic limit, we may assume that the tension in the spring is proportional to its modified in length from the equilibrium position. Then T = k x, where T is the spring force, k is constant and x is the change of length.
Let ax be the acceleration with which the spring shall come back to its equilibrium position. Adding up forces in horizontal direction, we have - T = max.
Please note that x is to the right, thus ax is written as positive and T is to the left, hence it is written as negative.
∴ - k x = m (d 2 x /dt2) - a Simple Harmonic Motion.
The solution of this second order differential equation may be written as following
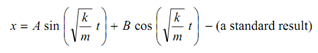
The values of A and B may be calculated as below. Value of x is x0, when t = 0.
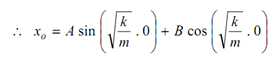
= 0 + B
∴ B = x0
and
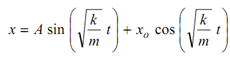
To evaluate A, we differentiate x w. r. t. time as we know v = 0, when t = 0.
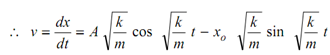
when t = 0, v = 0 and
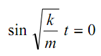
∴ we get A = 0.
∴ The equation of motion for this problem is