More Optimization Problems

Example   A window is being built in which the bottom is rectangle and the top is a semicircle. If there framing materials is 12 meters what have to the dimensions of the window be to let in the most light?

Solution

Let's ask this question again in somewhat easier to understand terms.  We desire a window in the shape defined above to contain a maximum area (and therefore let in the most light) and contain a perimeter of 12 m (since we have 12 m of framing material).  Little bit simple to understand in those terms.

Following is a sketch of the window.  h is height of the rectangular portion and since the semicircle is on top and width of the rectangular portion at 2r.

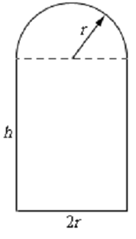
The perimeter (our constraint) refers for the lengths of the three sides onto the rectangular portion as well as half the circumference of a circle of radius r. The area (what we desire to maximize) is the area of the rectangle as well as half the area of a circle of radius r.  Following are the equations we'll be working with in this example.

Maximize : A = 2hr +  (½)∏ r ²

Constraint : 12 = 2h + 2r + ∏ r

In this case we'll solve out the constraint for h & plug that into the area equation.

h = 6 - r - 1/2 ∏ r ⇒  A (r )= 2r (6 - r - (1/2) ∏ r) + 1/2 ∏ r ²  =12r - 2r² - 1/2 ∏ r ² 

The first & second derivatives are,

A′ ( r ) = 12 - r ( 4 + ∏ )                   A′′ ( r ) = -4 - ∏

We can illustrates that the only critical point is,

                                      r = 12 /4 + ∏

We can also illustrate that the second derivative is always -ve (actually it's a constant) and so we can think that the maximum area should occur at this point. Therefore, for the maximum area the semicircle on top should have a radius of 1.6803 and the rectangle should have the dimensions 3.3606 x 1.6803 (h x 2r).