Matrix solutions to systems of the linear algebraic equations:

The linear algebraic equation is an equation of the form

a₁x_{1 +} a₂x₂ + a₃x₃   .  .  .  .  a_nx_n = b

Where a's are the constant coefficients, the x's are the unknowns, and b be constant. A solution is a series of numbers s₁, s₂, and s₃ which satisfy the equation. The illustration is as follows,

4x₁ +  5x₂ - 2x₃ = 16

is such an equation in which there are 3 unknowns: x₁, x₂, and x₃. The One solution to this equation is x₁ = 3, x₂ = 4, and x₃ = 8, as 4 * 3 + 5 * 4 - 2 * 8 is equal to 16.

The system of linear algebraic equations is a set of equations of the form:

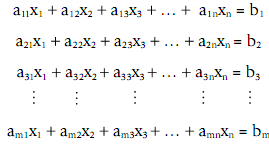
This is known as m × n system of equations; there are m equations and n unknowns.

As of the way that matrix multiplication works, such equations can be presented in matrix form as Ax = b here A is a matrix of the coefficients, x is the column vector of the unknowns, and b is the column vector of constants from the right-hand side of the equations:

A solution set is a set of all the possible solutions to the system of equations (all sets of values for the unknowns which solve the equations). All the systems of linear equations have either:

•  No solutions
•  One solution
•  Infinitely many solutions

The one of the main concepts of the subject of linear algebra is the various techniques of solving (or trying to solve!) systems of the linear algebraic equations. The MATLAB has many functions which assist in this process.

The system of equations has been once written in matrix form, what we want is to evaluate the equation Ax = b for the unknown x. To do this, we require to isolate x on one side of the equation. If we were working with scalars, then we divide both sides of the equation by x. However, with the MATLAB we can use the divided into operator to do this. Though, most languages cannot do this with matrices, therefore we rather multiply both sides of the equation by the inverse of the coefficient matrix A:

A^-1 A x = A^-1 b

Then, as multiplying a matrix by its inverse results in the identity matrix I, and since multiplying any matrix by I answers in the original matrix, we contain:

I x = A^-1 b

or

x = A^-1 b

This means that the column vector of unknown x is found as the inverse of matrix A multiplied by the column vector b. Therefore, if we can find the inverse of A, we can resolve for the unknown in x.