It is not the first time that we've looked this topic. We also considered linear independence and linear dependence back while we were looking at second order differential equations. Under that section, we were dealing along with functions, although the concept is fundamentally the same here. If we begin with n vectors,
x?1, x?2, x?3,.................., x?n
If we can get constants, c1,c2,...,cn with at least two nonzero as,
c1 x?1 + c2 x?2 + c3 x?3+..................+ cn x?n .............................(4)
Then we take the vectors linearly dependent. If the merely constants which work in (4) are c1=0, c2=0,..., cn=0 after that we call the vectors linearly independent.
If we additionally make the assumption as each of the n vectors has n elements that is each of the vectors seem as,
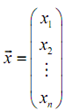
We can find a very simple test for linear independence and dependence. Remember that it does not have to be the case, although in all of our work we will be working along with n vectors each of that has n elements.
Fact
Provided the n vectors each with n components,
x?1, x?2, x?3,.................., x?n
From the matrix:
X = (x?1 x?2 ......... x?n)
Therefore, the matrix X is a matrix that ith column is the ith vector, xi. After that,
1. If X is nonsingular (that is det(X) is not zero) then the n vectors are linearly independent, nd
2. If X is singular (that is det(X) = 0) then the n vectors are linearly dependent and the constants which make (4) true can be determined by solving the system
xc? = 0? here c is a vector having the constants in (4).