Limit Comparison Test
Assume that we have two series ∑an and ∑bn with an, bn ≥ 0 for all n. Determine,
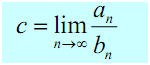
If c is positive (i.e. c > 0 ) and is finite (i.e. c < ∞ ) afterwards either both series converge or both of the series diverge.
Notice that it doesn't actually matter which series term is in the numerator for this test, we could just have easily illustrated c as,
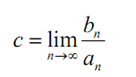
and we would get similar results. To observe why this is, consider the subsequent two definitions.

Initiate with the first definition and rewrite it as follows, afterwards take the limit.
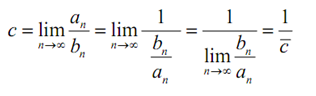
Alternatively, if ?c is positive and finite then so is c‾ and if c‾ is positive and finite then so is c. Similarly if c‾ = 0 then c = ∞ and if c‾ = ∞ then c = 0. Both of the above definitions will give similar results from the test so don't worry as regards which series terms should be in the numerator and that should be in the denominator. Select this to make the limit easy to calculate.
As well, this really is a comparison test in some other ways. If c is positive and finite this is saying that both of the series terms will behave in usually the same way and thus we can expect the series themselves to as well behave in an identical fashion. If c = 0 or c = ∞ we can't say this and thus the test fails to provide any information.
The limit in this test will frequently be written like this:
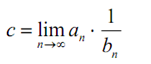
as frequently both terms will be fractions and this will build the limit easier to deal with.