Here is not too much to this section. We're here going to work an illustration to exemplify how Laplace transforms can be used to solve systems of differential equations.

Illustration:  Solve the following system.

x₁'= 3x₁ - 3x₂ + 2;                    x₁(0) = 1

x₂'= -6x₁ - t;                             x₂(0) = -1

Solution:

First see that the system is not specified in matrix form. This is since the system won't be solved in matrix form.  Also notice that the system is nonhomogeneous.

We start just as we did while we used Laplace transforms to resolve single differential equations. We get the transform of both differential equations.

sX₁(s) - x₁(0) = 3x₁(s) - 3x₂(s) + (2/s)

sX₂(s) - x₂(0) = -6x₁(s) - (1/s²)

Here plug into the initial condition and simplify things a little,

(s - 3)X₁(s) + 3X₂(s) = (2/s) + 1 = (2 + s)/s

6X₁(s) + sX₂(s) = -(1/s²) - 1 = -((s²+ 1)/s²)

Here we require solving this for one of the transforms.  We'll do that by multiplying the top equation by s and the bottom with -3 and after that adding. It gives,

(s² - 3s - 18) X₁(s) = 2 + s + ((3s²+ 3)/s²)

Solving for X₁ provides,

X₁(s) =(s³ + 5s3 + 3)/(s² (s + 3)( S -6))

Partial fractioning provides,

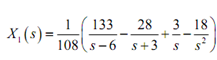
Taking the inverse transform Taking the inverse transform gives us the first solution us the first solution,

x₁(t) = (1/108) (133 e^6t - 28 e^-3t + 3 - 18t)

Here to find the second solution we might go back up and remove X₁ to get the transform for X₂ and sometimes we would require doing that. Though, in this case notice that the second,

x₂'= -6x₁ - t                  ⇒                     x₂ = ∫(- 6x1 - t) dt

Therefore, plugging the first solution into and integrating gives,

x₂(t) = -(1/18) ∫ (133 e^6t - 28 e^-3t + 3t) dt

 = -(1/108) (133 e^6t - 28 e^-3t + 3 - 18t) + c

Here, reapplying the second initial condition to find the constant of integration provides,

-1 = -(1/108) (133 + 56) + c                ⇒                                 c = ¾

Then the second solution is,

x₂(t) = -(1/108) (133 e^6t - 56 e^-3t + 18t - 81)

Therefore, putting all this together provides the solution to the system as,

x₁(t) = (1/108) (133 e^6t - 28 e^-3t + 3 - 18t)

x₂(t) = -(1/108) (133 e^6t - 56 e^-3t + 18t - 81)

Compared to the previous section the work here wasn't very bad. This won't all the time be the case of course, but you can notice that using Laplace transforms to determine systems isn't very bad in at least several cases.