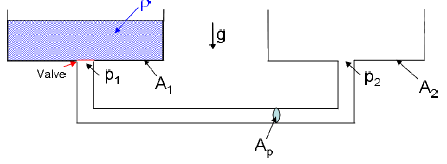
Two reservoirs of equal cross sectional areas (315 m²) and at equal elevations are connected by a pipe of length 20 m and cross sectional area 3 m². The reservoir on the left (reservoir 1) is filled with a liquid of mass density 1000 kg/m³. The pressure at the bottom of reservoir 1 (that is, p₁) is 39000 N/m2. The second reservoir and the connecting pipe are initially empty. The acceleration due to gravity is 9.8 m/s².

The following assumptions apply. One can ignore the effects of friction, form losses and the elevation differences along the path of the connecting pipe. The fluid is incompressible and inviscid. Flow through the connecting pipe is started by the instantaneous, full opening of the valve at the bottom of reservoir 1.

Using the finite difference method, write a Fortran program that predicts the behavior of the system for 200 seconds following the opening of the valve. Assume a timestep size of

0.1 sec. The program must read the above data (with the exception of the acceleration due to gravity and problem duration time of 200 seconds) from an input file and generate an output file. Run the following four cases;

a) one for the above data,

b) identical to case (a) but with the cross-sectional area of the second reservoir, A₂, modified to 200 m₂,

c) identical to case (a) but with the length of the connecting pipe, L, modified to 40 m, and

d) identical to case (a) but with the cross sectional flow area of the connecting pipe, Ap, modified to 6 m2.

The output file must include the following information:

Modeling and Simulation for Mechanical and Nuclear Engineers -

• the date and time of the run,
• a summary of the input data values, including units of measurement,
• the maximum value of the volumetric flow rate, qv, through the connecting pipe(m³/s),

• the maximum depths of the water in meters in each reservoir during the transient,
• the maximum pressure at the exit of each reservoir (p₁ and p₂) during the transient (N/m²), and
• a table of the volumetric flow rate through the connecting pipe (m³/s), the depth of water in each reservoir in meters, and the pressures p₁ and p₂ as a function of time.

The deliverables are:

• the Fortran source code listing,
• the input and output files for the four cases, and
• the following plots as a function of time for each case:

the volumetric flow rate through the connecting pipe,

a comparison of the values of p₁ and p₂, and

a comparison of the fluid depth in each reservoir.

Plots should have appropriately labeled axes. The y-axis parameter value may be normalized if you wish.

In the text of the transmitting email answer the following:

1. explain the differences in the results of the four cases in terms of changes to the system's fluid capacitance Cf and fluid inductance If, and

2. Explain how this system relates to that of the unsteady flow in a U-tube discussed in class. For example, all else being equal, does the period of oscillation of the liquid in this system, like that of the U-tube system, vary as the square root of the length of the connecting pipe? Back up your answer either by reference to the required cases or to additional cases that you run.