We contain a piece of cardboard i.e. 14 inches by 10 inches & we're going to cut out the corners as illustrates below and fold up the sides to form a box, also illustrated below. Find out the height of the box which will give a maximum volume.
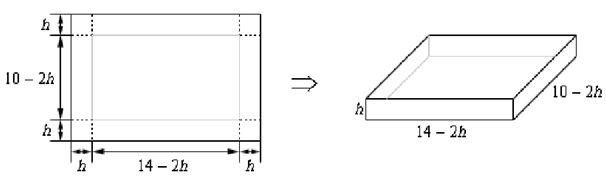
Solution : In this instance, for the first time, we've run into problem where the constraint doesn't actually have an equation. The constraint is just the size of the piece of cardboard and has been factored already into the figure above. It will take place on occasion and therefore don't get excited about it when it does. It just means that we have one less equation to worry about. In this case we desire to maximize the volume. Following is the volume, in terms of h and its first derivative.
V ( h ) = h (14 - 2h ) (10 - 2h ) = 140h - 48h2 + 4h3
V ′ ( h ) = 140 - 96h + 12h2
Setting the first derivative equivalent to zero & solving gives the following two critical points,
h = (12 ±√39)/3 = 1.9183, 6.0817
Now we have clear problem. We have two critical points & we'll have to determine which one is the value we required. In this case, it is easier than it looks. Go back to the figure in the difficulty statement & notice that we can quite simply determine limits on h. The smallest h can be is h = 0 even though it doesn't make much sense as we won't obtain a box in this case. Also from the 10 inch side we can illustrate that the largest h can be is h = 5 although again, it doesn't make much sense physically.
Thus, knowing that whatever h is it has to be in the range 0 ≤ h ≤ 5 we can illustrates that the second critical point is outside of this range and thus the only critical point that we required to worry about is 1.9183.
At last, as the volume is described and continuous on 0 ≤ h ≤ 5 all we have to do is plug in the critical points & endpoints into the volume to find out which gives the largest volume. Following are those function evaluations.
V (0) = 0 V (1.9183) = 120.1644 V (5) =0
Therefore, if we take h = 1.9183 we obtain a maximum volume.