Q. Explain the problem with IS-LM model?

The starting point of AS-AD model is an assumption in IS-LM model (and in the cross model) that limits its usefulness. This is an assumption that if firms where to choose profit maximizing quantity of L (L_OPT), they would produce more than aggregate demand. In IS-LM, Y_OPT> YD should hold.

To realize why it is a problem in IS-LM model, we gradually increase aggregate demand by increasing G. We can explain the process using figure below.

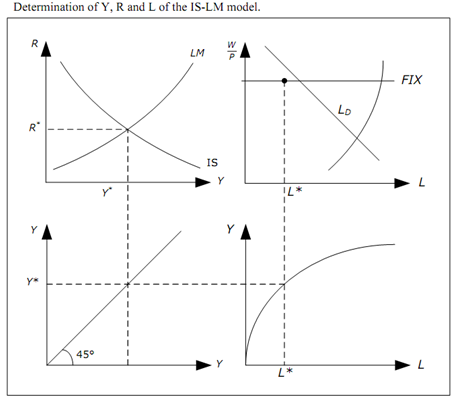
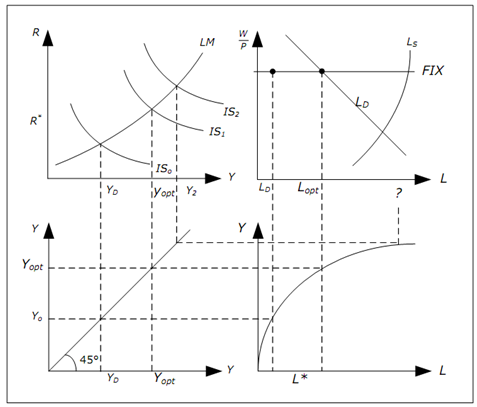
Figure: Illustrating the problem in the IS-LM model

1. Let's begin with a given real wage W/P, an IS curve (IS₀) and an LM curve. In equilibrium, we would have Y = Y₀ and L = L₀.

2. Now increase G so that IS curve shifts outwards from IS₀ to IS₁. In the first step, we increase G just enough so that Y = Y_OPT in equilibrium It implies exactly to the level that firms want to produce at the given real wage.

3. Firms would now want to hire L_OPTthat is precisely the profit-maximizing quantity of L. It is no longer essential for firms to hire less than profit maximizing quantity as there is no longer a shortage in aggregate demand. Thus far, no problems in IS-LM model. 

4. Now imagine that we increase G even more so that IS curve shifts to IS₂ such that Y = Y₂> Y_OPT. Now IS-LM model is in trouble. 

5. According to production function, to produce Y = Y₂ we need L = L₂. However firms will only hire L_OPT if real wage is constant (that is presumed in IS-LM model). L_OPT is the profit maximizing quantity - to produce more would decrease profits. 

6. As firms won't hire more than L_OPT if real wages are constant, GDP can't be larger than of Y_OPT in the IS-LM model. This model simply can't give an answer to what will happen when we increase G in step 4 as we would be violating one of the main assumptions of IS-LM model. 

This problem isn't limited to changes in G and shifts in IS-curve. The same problem appears when we change MS and shift LM-curve. If we shift LM-curve to the right by an amount such that Y > Y_OPT, the IS-LM model can't be used. 

IS-LM model isn't 'wrong', but it's applicable only as long as Y > Y_OPT. Normally the IS-LM model will perform reasonable as long as price level is stable (low inflation) and it will do better in a recession than in a boom.