A piece of pipe is carried down a hallway i.e 10 feet wide.  At the ending of the hallway the there is a right-angled turn & the hallway narrows down to 8 feet wide. What is the longest pipe which can be carried (always keeping it horizontal) around the turn in the hallway?

Solution

Let's begin with a sketch of the situation therefore we can obtain a grip on what's going on and how we will solve this.

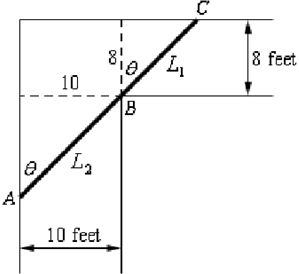
The largest pipe which can go around the turn will do therefore in the position illustrates above.  One end will be touching the outer wall of the hall way at A & C and the pipe will contact the inner corner at B. Let's suppose that the length of the pipe in the little hallway is L₁  while L₂  is the length of the pipe into the large hallway. Then the pipe has a length of L = L₁ + L₂ .

Now, if θ = 0 then the pipe is totally in the wider hallway and we can illustrates that as θ → 0

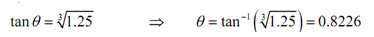
then L → ∞ .  Similarly, if θ = ∏/2 the pipe is totally in the narrow hallway and as θ → ∏/2   we also have L → ∞ .  Therefore, somewhere in the interval 0 < θ < ∏/2    is an angle that will minimize L and oddly sufficient i.e. the length that we're after. The largest pipe which will fit around the turn will actually be the minimum value of L.

The constraint for this problem is not so obvious and there are in fact two of them.  The constraints for this difficulty are the widths of the hallways.  We'll utilize these to obtain an equation for L in terms of θ & then we'll minimize this new equation.

Therefore, by using basic right triangle trig we can illustrates that,

L₁ = 8 sec θ           L₂  = 10 csc θ        ⇒       L = 8 sec θ + 10 csc θ

Therefore, differentiating L gives,

                           L′ = 8 sec θ tan θ -10 csc θ cot θ

Setting this equivalent to zero and solving out specified,

                    8 sec θ tan θ = 10 csc θ cot θ

sec θ tan θ /csc θ cot θ = 10/8

sin θ tan² θ /cos θ =5/4           ⇒         tan3 θ = 1.25

Solving for θ gives,

Therefore, if θ = 0.8226 radians then the pipe will contain a minimum length and will just fit around the turn. Anything larger will not fit about the turn that's why the largest pipe that can be carried around the turn is,

                              L = 8 sec (0.8226 ) + 10 csc (0.8226) = 25.4033 feet