Example   Evaluate following limits.

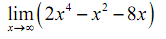
Solution

Here our first thought is probably to just "plug" infinity into the polynomial & "evaluate" every term to finds out the value of the limit.  This is pretty simple to illustrate what each term will do in the limit and so this look likes an obvious step.

Hence, let's see what we obtain if we do that.  As x approaches infinity, then x to a power can just get larger and the coefficient on each of the term (the first and third) will jsut make the term even larger. Hence, if we look at what each of the term is doing in the limit we get the following,

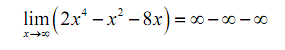
Now, we've obtained a small, although easily fixed, problem to deal along with. Probably we are tempted to say that the answer is zero (since we have infinity minus infinity) or possibly -∞ (as we're subtracting two infinities off of one infinity).  Though, in both of the cases we'd be wrong

Infinities only don't always behave as real numbers do while it comes to arithmetic.  Without more work there is no way to know what ∞ -∞ will be and hence we really have to be careful along with this kind of problem. 

Hence, we require a way to get around this problem.  What we'll do here is factor out the largest power of x out of the whole polynomial as given,

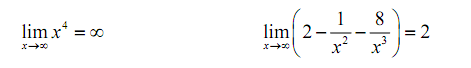
Now for each terms we have,

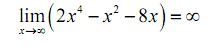
The first limit is obviously infinity and for the second limit we'll use the fact above on the previous two terms. Hence by busing Fact 2 from the previous section we see value of the limit will be,

Fact 2

If  p ( x ) = a_n xⁿ + a_n-1 x^{n -1} + ....... + a ₁x + a₀ is a polynomial of degree n (that means  a_n  ≠ 0 )  then,

What this fact is actually saying is that while we go to take a limit at infinity for a polynomial then all we have to really do is look at the term along with the largest power and asks what that term is doing in the limit as the polynomial will have the similar behavior.

Let's now move into some more complexes limits.