Solve the subsequent IVP.

cos(x) y' + sin(x) y = 2 cos³(x) sin(x) - 1

y(p/4) = 3√2, 0 < x< p/2

Solution:

Rewrite the differential equation to determine the coefficient of the derivative an individual.

y' + (sin(x)/cos(x))y = 2cos² (x) sin(x) - 1/cos(x)

y' + tan(x)y = 2cos² (x) sin(x) - sec(x)

Now determine the integrating factor:

Can you do the integral? If not rewrite tangent back in sines and cosines and after that use a easy substitution. Remember that we could drop the absolute value bars upon the secant due to the limits on x.  Actually, this is the purpose for the limits on x.

Also remember that we made use of the subsequent fact.

e^Inf(x) = f(x)    .........................(11)

It is a significant fact that you must always keep in mind for these problems. We will want to make simpler the integrating factor as much as probable in each case and this fact will assist with which simplification.

Currently back to the illustration. Multiply the integrating factor by the differential equation and confirm the left side is a product rule. Notice also that we multiply the integrating factor by the rewritten differential equation and NOT the original differential equation. Ensure that you do that. If you multiply the integrating factor via the original differential equation you will find out the wrong solution!

sec(x) y' + sec(x) tan (x)y = 2sec(x) cos²(x) sin(x) - sec²(x)

(sec(x) y)' = 2cos(x) sin(x) -sec²(x)

Integrate both sides.

∫(sec(x) y)' dx = ∫(2cos(x) sin(x) -sec²(x)) dx

sec(x) y(x) = ∫ sin(2x) - sec²(x) dx

sec(x) y(x) = - ½  cos(2x) - tan(x) + c

See there the use of the trig formula sin (2q) = 2 sin q cosq resolve for the solution.

y(x) = - ½ cos(x) cos(2x) - cos(x) tan(x) + c cos(x)

= - ½ cos(x) cos(2x) - sin(x) + c cos(x)

At last, apply the initial condition to determine the value of c.

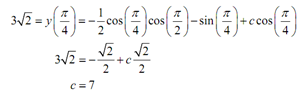
The solution is afterward as:

y(x) =  - ½ cos(x) cos(2x) - sin(x) + 7 cos(x)

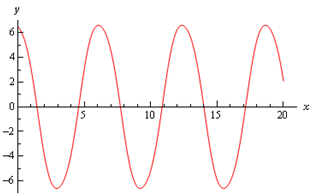
A plot of the solution is here given below: