Determine the centroidal moment of inertia:

Determine the centroidal moment of inertia of a thin flat disc shown in Figure which is having a mass m kg. By using the parallel axis theorem, extend the result of cylinder of radius a and height h.

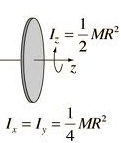
Solution

We let the disc made up from rings of varying radius r and thickness dr as illustrated in the figure. The mass of each such ring per unit length shall be m¯ dr . The moment of inertia of this ring can be written as if dm = mass of one such ring then dm = 2πrdr m¯ .

=2 π m¯ a ⁴ /4

 = π a ²  m¯ .( a²/2)

Substituting m = π a ² m¯ , total mass of the disc, we get

I z_o= m .(a²/2)

and

= I x_o = Iy_o  = (1/ 4) ma²

and radius of gyration

kx_o       = ky_o = (½) a

The moment of inertia of the cylinder of Figure (b) about the axes x, y, z may be calculated by extending the above results. The cylinder may be imagined to consist of thin discs of thickness dz.

Suppose   γ = unit mass/volume

The total mass of the disc dm = π a ²  dz . γ . The moment of inertia of the disc about its own centroidal axes shall be

I z_o = 1 dm . a ²  = 1 π γ a ⁴  dz

I x_o       = I y_o = (1 /4)π γ a ⁴  d z

Using parallel axes theorem, the moments of inertia of the disc around the axes x, y,

z are found as

I _z = ∫ (½ ) π γ a ⁴  dz

I _x = I _y  = ∫(1/4) π γ a ⁴  dz + π γ a ²  z ²  dz

Integrating between the limits

z = - (½) h  to   z = + (½) h

gives,

 I _z  = (γ π a ⁴  h )/2

I _x = I _y  = (¼) γ π a⁴   h + (1/12) γ π a²  h

The total mass of the cylinder m = γ π a ²  h , so the above results may be written as

I _z  = ma²/2  , I x  = I y = (ma⁴/4) + ( 1/12)  mh ²

A sphere is having a radius R and mass m. calculate the moment of inertia about its diameter.