Thus, just why do we care regarding direction fields? Two nice pieces of information are there which can be readily determined from the direction field for a differential equation.

1. Sketch of solutions. As the arrows in the direction fields are actually tangents to the actual solutions to the differential equations we can utilize these as leads to sketch the graphs of solutions to the differential equation.

2. Long Term Behavior. In several cases we are less interested in the actual solutions to the differential equations so we are in how the solutions behave as t raises. Direction fields, if we can find our hands on them, can be utilized to determine information regarding this long term behavior of the solution.

Here back to the direction field for our differential equation. Assume that we need to know what the solution that has the value v (0) = 30 looks like. We can be there our direction field and begin at 30 on the vertical axis. At that point we know that the solution is raising and that as it rises the solution should flatten out since the velocity will be approaching the value of v = 50. So we create drawing a raising solution and while we hit an arrow we just ensure that we stay parallel to such arrow. This provides us the figure as given below.

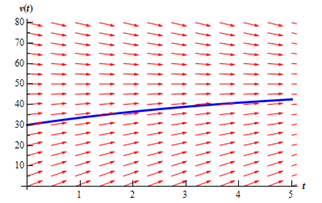
To find a better notion of how all the solutions are behaving, here we put a few more solutions in. Adding several more solutions gives the figure as given below. The set of solutions that we've graphed below is often termed as the family of solution curves or the set of integral curves. The number of solutions which is plotted while plotting the integral curves varies. You must graph sufficient solution curves to demonstrate how solutions in each portions of the direction field are behaving.

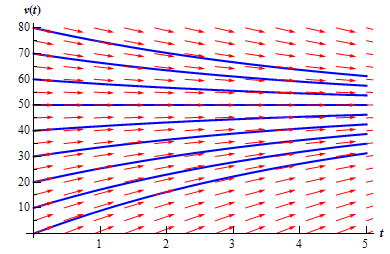
Here, from either the direction field or the direction field along with the solution curves sketched in we can notice the behavior of the solution as t raises. For our falling object, this looks like all of the solutions will approach v = 50 as t raises.

We will frequently need to know if the behavior of the solution will base on the value of v(0).  In such case the behavior of the solution will not depend upon the value of v (0), although that is possibly more of the exception than the rule so don't specific that.