Reference no: EM132870489
Task
In this practice, we will implement the Breadth First Search and Depth First Search Algorithms.
i) First, we want a structure to represent the graph. We are going to use the adjacency list representation for graph. We are going to declare a dictionary G to represent the graph and the keys in the dictionary are going to be the nodes in the graph. The values associated with a key is a list of vertices that are adjacent to the vertex specified in the key. For example, if we have the following graph the dictionary is going to be, G = {‘P': [‘Q','R'], ‘Q': [‘P','R'], ‘R': [‘P','Q']}

Note: While defining your graph like this if there is no adjacent node then you need to have an empty list
ii) We discussed about the BFS algorithm in class. Write a python function called BFS that takes graph and the starting vertex, and returns a BFS order (as a list) of the graph.
Note:
a. Create a list to store the visited vertices. The BFS function returns this list.
b. The BFS algorithm uses a Queue and a Set. We will use python list and set data types to implement these data structures. Select the right methods for list so the you can mimic the behavior of a queue.
iii) We also discussed about the DFS algorithm in class. Write a python function called DFS that takes the graph and the starting vertex, and returns a DFS order (as a list) of the graph.
Note:
a. Create a list to store the visited vertices. The function returns this list.
b. The DFS algorithm uses a Stack and a Set. We will use python list and set data types to implement these data structures. Select the right methods for list so the you can mimic the behavior of a stack.
iv) Write a main function, and create the following graph
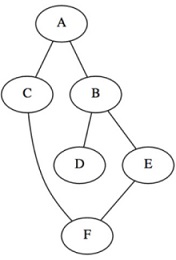
v) Call the BFS and DFS function to print the BFS and DFS orders of the graphs.
vi) Device an algorithm also to detect a cycle in a graph. For example, the graph above has a cycle (A-B-E-F-C-A). Write a function cycle_detect that takes a graph as input and returns true if there is a cycle and false otherwise.