What is the value of the correlation coefficient

Assignment Help Applied Statistics

Reference no: EM132299864

QUESTION 1

A published paper by Tuzson et al. (2003) in Archives of Physical Medicine and Rehabilitation (vol. 84, pp. 1363-1368) examined the peak knee velocity in walking (measured in degrees per second) at flexion (x) and extension (y) for 18 subjects with cerebral palsy. The relationship between the two variables is illustrated in the scatter plot below.

Below are the summary statistics for peak knee velocity at flexion and extension.

∑ x = 4880, ∑y = 4710, ∑x 2 = 1553300, ∑y² = 1437700 and ∑xy = 1468725

(a) Calculate the sum of squares totals Sxx, Syy, and Sxy.

(b) What is the value of the correlation coefficient r? Comment on the strength and direction of the linear relationship.

(d) What is the value of the coefficient of determination? How much variability in knee velocity at extension is explained by knee velocity at flexion?

(e) Below are the Q-Q plot for the residuals (left) and the residual plot (right).

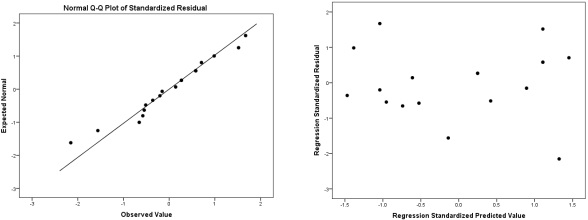
Using the above graphs, comment as to whether the assumption of normality and constant variances are valid for this regression model.

(f) Perform a hypothesis test to test whether to test whether the population slope parameter β1 = 0 (you can use either the t- or ANOVA approach).

(g) What is the expected knee velocity at extension of a subject with cerebral palsy whose knee velocity at flexion was 290 degrees/second?

(h) What is the 95% confidence interval for the knee velocity at extension of a subject with cerebral palsy whose knee velocity at flexion was 290 degrees/second?

(i) What is the 95% prediction interval for the knee velocity at extension of a subject with cerebral palsy whose knee velocity at flexion was 290 degrees/second?

QUESTION 2

Dual-energy X-ray absorptiometry (DXA) is a method that uses X-rays of two different energies to estimate a person's body fat percentage (% body fat). The X-ray scans take approximately 10 minutes and the amount of radiation is very low. The advantage of using this method is that it provides accurate % body fat measurement, along with other information including bone density, lean mass and fat readings for different part of the body (e.g. arms, legs and torso). However, this option can be expensive and is typically only available in medical or research settings, and not to the general public.

The SPSS/PSPP file named "ElderlyPopWA.sav" contains data pertaining to the % body fat, waist circumference (cm), hip circumference (cm), tricep skinfold (mm) and arm girth (cm) measurements of 148 elderly females (mean age 74.3 ± 2.6 years; mean BMI 26.6 ± 3.9 kg/m²) in Western Australia. The majority of women in this study are either overweight or obese (65% with BMI >25 kg/m²). The objective here is to determine whether one can develop a regression model based on waist and hip circumference, tricep skinfold and arm girth measurements for predicting % body fat percentage of elderly women based on these four easier to obtain measurables.

Using the given dataset (you may ignore the age and BMI data), perform multiple linear regression modelling in SPSS and answer the following questions.

(a) What is the multiple correlation coefficient and the coefficient of multiple determination? Explain what each of these terms mean, and comment on their value.

(b) What is the equation of the line of best fit relating the body fat percentage with the other variables?

(c) Examine the ANOVA table in the SPSS output. What are the null and alternate hypotheses corresponding to the results of this ANOVA table? What can you conclude based on the results shown in this table?

(d) Which of the variables are significant predictors of body fat percentage? Explain your reasoning.

(e) Below are the normality test result on the residuals (left), along with the residual plot (right). Do the assumptions of normality and constant variance hold? Justify.

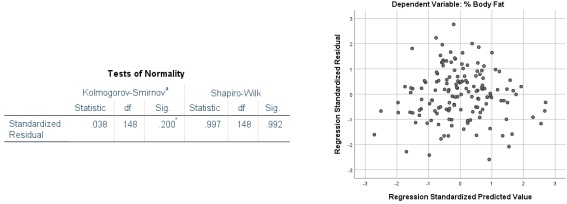
(f) Predict the body fat percentage of a 45 year old female who has a weight circumference = 75 cm, hip circumference = 82.5 cm, tricep skinfold 17.5 mm and an arm girth of 37 cm. Comment on the validity of this estimate?

QUESTION 3

A study of lower back pain in a particular industry looked at the effect of the type of work (i.e. Manual or Non- Manual) on the severity of back pain in the past six months. The data were as follow:

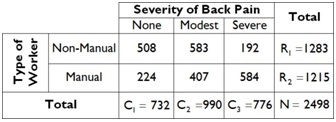
Perform a Chi-square independence test (by hand) at the 5 % level of significance to determine whether there is a relationship between the severity of back pain and the type of work in this particular industry. If so, which type of work tends to have a greater proportion of workers with severe back pain?

Make sure you state the relevant hypotheses, test statistic, p-value and a concluding statement regarding your finding.

QUESTION 4

For Q3 of Assignment 1, you would have noticed that the assumption of normality does not hold for the pollutant CO. Given this, perform the appropriate non-parametric test (by hand) and determine whether there is a difference in CO measured by the QCMD as compared to the ground truth at the 5 % level of significance. The relevant data are given in the Excel file "CO.xlsx".

Make sure you state the relevant hypotheses, test statistic, p-value and a concluding statement regarding your finding.

Attachment:- Assignment.rar

Reference no: EM132299864

Questions Cloud

Define process of translating research into practice : The bases for the theory are then an observation has been made and that when these certain things share the ct same space and time a particular thing is likely.

How would you go about implementing the theory of hope : Interesting article, Joseph (2015) talks about theories that promote positive psychology. One of the theory is hope and uses the Harry Potter series.

Name some statistical packages that are available : NURS 605- Epidemiologic Methods for Health Promotion and Disease Prevention Assignment, Walsh University, USA. Name some statistical packages that are available

Discuss your rationale for the interventions identified : Provide substantiating evidence (assessment data) for each problem identified. Identify and describe at least four medical and/or nursing interventions.

What is the value of the correlation coefficient : MAT5212 - Biostatistics - Edith Cowan University - What is the value of the correlation coefficient r? Comment on the strength and direction of the linear

Describe the policy or regulation you selected : As a professional nurse, you are expected to apply your expertise to patient care. On occasion, you will also be expected to share that expertise.

How stable is temperament over the life span : Researchers who work from this perspective search for identifiable, enduring patterns of behavior and thought processes that seem to apply to all people.

Describe the results or aspects of the three measures : Describe the results or aspects of the three measures you see as valuable and why. Describe what enhancements to your mental health you might expect.

Calculate appropriate estimate of mean hospitalisation cost : Calculate the appropriate estimate of the mean hospitalisation cost and its associated 95% confidence interval before the intervention

Reviews

len2299864

5/5/2019 11:17:16 PM

The following factors will NOT be considered as grounds for extension: • Routine demands of employment; • Stress or anxiety normally associated with examinations, required assessments or any aspect of course work; • Routine financial support needs; • Lack of knowledge of the requirements of academic work; • Difficulties with English language; • Scheduled anticipated changes of address, moving home etc; • Demands of sport, clubs, social or extra-curricular activity other than those specified above; • Recreational travel (domestic or international); • Planned events such as weddings, birthday parties etc; • Misreading the deadline

len2299864

5/5/2019 11:17:10 PM

CONDITIONS FOR ASSIGNMENT EXTENSION In accordance with ECU policy, extensions are given on the following grounds and must include all appropriate supporting documentation: • Ill health or injury for an extended period of time – medical certificate is required; • Compassionate grounds – supporting documentation includes e.g. newspaper notice plus other evidence if not the same family name, e.g. marriage certificate; • Representation in sporting activities at a national or international level; • Representation in significant cultural activities; • Employment related intrastate, interstate and overseas travel – a letter from your employer, including your supervisors’ full contact details.

len2299864

5/5/2019 11:17:02 PM

4. All questions must be presented in the order given. Failure to do so will result in your assignment NOT being marked. 6. Be clear and concise. Show all of your working for hand calculation questions. Full marks will only be awarded to correct answers with complete solutions. All manually calculated answers are to be presented correct to 3 decimal places (make sure you understand the rounding rules). Worded answers need to be written or typed up in grammatically correct English. Failure to do so will result in deduction of marks. 7. Copy only the relevant tables and charts from the SPSS output across to your solution document, and these must be interpreted appropriately and in the context of the study. 8. In the interest of fairness, extension of time for submission of the assignment will be given only in exceptional circumstances, and then only in accordance with University rules (see page 2).

len2299864

5/5/2019 11:16:54 PM

SUBMISSION GUIDELINES: 1. This assignment constitutes 20% of the assessment for this unit and has a total mark of 45. 2. All students are to hand in a softcopy assignment via Turnitin on Blackboard. Solutions to all questions in the assignments must be presented in in ONE word or pdf file or your assignment will NOT be marked. 3. Turnitin is a tool for students and academics to check the ‘originality’ of their work. It is strongly recommended that you submit your assignment (or a late draft) for a Turnitin preview at least 48 hours before the actual due date. This should allow you enough time to receive your Turnitin originality report, and if required, make changes to your work and review it once more. The more time you allow yourself, the less likely the chance that you will end up involved in a breach of academic integrity rules. Once you ‘Submit’ your assignment, you are agreeing that you understand university rules and expectations around academic integrity, writing and referencing and that you have taken all necessary steps to ensure your work is authentic and your own.

Write a Review

Required(*) Message

Assured A++ Grade

Get guaranteed satisfaction & time on delivery in every assignment order you paid with us! We ensure premium quality solution document along with free turntin report!

Submit Assignment

User Account

All Pages