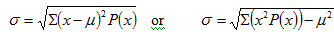Reference no: EM13616

1. Listed below are the numbers of people executed in the United States from 1976   to 1994. (In 1976, the U.S. Supreme Court allowed the death penalty to be carried out.)

Number of Executions	Number of Years
0 - 9	8
10 - 19	5
20 - 29	4
30 - 39	2

a) In how many years were 9 or fewer people executed?

b) If you choose a year at random, what is the probability that between 10 and 19 people were executed in that year?

c) If you pick three years at random, what is the probability that in all three of those years between 10 and 19 people were executed? (Be careful; you are sampling without replacement.) (Hint: do the probabilities for the second choice depend on the result of the first choice?)

d) If you pick three years at random what is the probability that in two of those years between 10 and 19 were executed, and in one of those years at least 30 were executed? (Be careful; you are sampling without replacement.)

e) If you pick three years at random what is the probability that in at least two of those years between 10 and 19 were executed?

2. A life-insurance company sells a term insurance policy to a 21-year-old male. The policy pays $100,000 if the insured male dies within the next five years. The probability that a randomly chosen male will die each year can be found in mortality tables. The company collects a premium of $250 each year as payment for the insurance. The amount X that the company earns on this policy is the product of $250 and the number of annual payments, less the $100,000 that it must pay if the insured male dies. The table below gives the relevant probabilities. (For instance, if the insured person dies while still 21, the insurance company earns [$250 (from the only premium) - $100,000], or - $99,750; the probability of this outcome is 0.00183.)

a) How could we know the relevant probabilities.

b) Fill in the missing column.

c) Calculate the expected amount earned by the insurance company from this single policy.

d) Calculate the variance and standard deviation.

e) Calculate the relative risk (σ/E) for a single policy. 

age at death	21	22	23	24	25	≥26
payout X (in $)	-99,750	-99,500	-99250	-99,000	-98,750
probability	0.00183	0.00186	0.00189	0.00191	0.00193

3. Suppose that you insure two 21-year-old males, and that their ages at death are independent. If we use X and Y for the insurer's incomes from the two insurance policies, then the total income is T = X + Y. Use the expected value and variance from the previous question.

a) Calculate the expected value, variance, and standard deviation of the total income T.

b) Determine the relative risk (σ/E) for T.

c) How many policies must you sell so that the relative risk is 10% of the expected value? 

4. At a grocery store, eggs are sold in cartons that hold 12 eggs. Experience suggests that 78.5% of all cartons contain no broken eggs, 19.2% have exactly one broken egg, 2.2% have exactly two broken eggs, and 0.1% have exactly three broken eggs. The fraction of cartons with four or more broken eggs is tiny.

A carton is selected at random, and an egg is selected at random from this carton. This egg is broken.

a) Construct a tree diagram illustrating two events:

1) select a carton, and

2) select an egg. Show all the joint outcomes. 

b) Calculate the joint probability of selecting a carton with 1 broken egg, and choosing the broken egg from that carton.  Express your calculation using the general rule of multiplication.

c) What are the four joint outcomes in which you choose a broken egg?

d) Calculate the probability of finding at least one broken egg in your carton. Express your calculation using the notation of conditional probability, and the general rule of multiplication.

e) Imagine selecting a carton. Someone looks inside and sees a broken egg.

Calculate the (conditional) probability that the broken egg is the only broken egg in this carton. (In other words, calculate the probability that you have chosen a carton with only one broken egg, given that you know there is at least one broken egg in the carton.) Express the calculation in the notation of conditional probability.

5. The industry journal Oil & Gas discussed the following case of prospect fields producing oil (Oil &Gas, January 11, 1988; cited in Anderson, Sweeny, and Williams, Statistics for Business and Economics, 7^th edition, p 170). A geological assessment indicated a 25% probability that a particular field would produce oil. There was an 80% probability that a particular well will strike oil, given that oil is present in the prospect field.

a) Construct a tree diagram. Show the selection of a well in the first column, and the result of drilling in subsequent columns.

b) Suppose a well is drilled and it does not strike oil. Calculate the probability that the field really does have oil.

c) If two wells come up dry, what is the probability that the field has oil?

d) The oil company would like to keep looking as long as the probability that the field has oil is greater than 1%. How many dry wells must be drilled before the field is abandoned?

6. Twenty-nine percent of American judges and lawyers are women (Statistical Abstract of the United States, 1997; cited in Anderson, Sweeney, and Williams, Statistics for Business and Economics, 7^th edition, p 197). Imagine a sample of 20 judges and lawyers.

a) Briefly explain why you would expect the number of number of women in a  group of 20 lawyers to be described by a binomial distribution. Refer to the four characteristics of a binomial distribution.

b) In this  example, would you expect the Poisson distribution to approximately describe  the number of women? Why or why not?

c) Draw a probability histogram, using the binomial tables and a 30% probability-of-success-on-a-single-trial. d) Using the binomial-probability formula, calculate the probability that 9 of these lawyers and judges are women. Use30% probability-of-success- on-a-single-trial. Compare your answer to the value in (c) above.

e) Use the binomial tables to calculate the probability that at least 9 of the lawyers and judges in the sample of twenty are women.

f) Calculate the expected number of lawyers and judges who are women (in a sample of 20). Use a 30% probability-of-success-on-a-single-trial.

g) Calculate the standard deviation of this distribution. Show your result on the histogram in (b). The standard deviation of a binomial distribution is

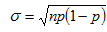
Use a 30% probability-of-success-on-a-single-trial. Show on the histogram in (c).

7. After the Space Shuttle Challenger exploded in 1986, the U.S. Air Force estimated the probability of a "disaster" on a single flight to be 1/34. The Challenger was the 25th flight.

a) Is the number of disasters that occur in a sample of 25 flights described by a binomial distribution? Discuss the four characteristics of a binomial distribution from class.

b) NASA kept flying shuttle missions until the first disaster occurred. Is the number of safe missions in THIS case described by a binomial distribution? Explain.

c) Calculate the probability that one flight in a group of 25 will end in disaster.

d) Calculate the probability that exactly two flights (in a group of 25 flights) end in disaster.

e) Calculate the probability of AT LEAST one disaster in 25 flights.

f) Construct a binomial probability histogram for the number of disastrous flights in a sample of 25. (Use a table of binomial probabilities.)

8. Refer to Question #7.

a) Calculate the expected number of disasters in 25 flights.

b) Imagine that the probability of a particular number of disasters is described by a Poisson distribution. Use your result in (c) to calculate the probability of at least one disaster in 25 flights.

c) Briefly explain why the number of disasters that occur in a sample of 25 flights should be described approximately by a Poisson

distribution.

d) Construct a Poisson probability histogram for the number of disastrous flights in a sample whose expected value is given in (a) above.

e) Is the histogram in (d) approximately the same as the histogram in question #7 above?

9. The number of cases of diptheria reported in the United States in any particular year between 1980 and 1987 is described by a Poisson distribution whose mean is 2.5 (Centers for Disease Control, "Summary of Notifiable Diseases, United States, 1989", Morbidity and Mortality Weekly Report, Volume 39, October 5, 1990; cited in Pagano and Gauvreau, Principles of Biostatistics,1st edition, p 170).

a) Calculate the probability that exactly four cases are reported in a particular year. Use both the Poisson tables and the Poisson formula.

b) Calculate the probability that no more than four cases are reported in a particular year.

c) Draw TWO probability histograms for the number of diptheria cases in any particular year.

(i) Use one of the histograms to illustrate the probability in (a) (i.e. the probability that exactly four cases are reported in a particular year).

(ii) Use the second histogram to illustrate the probability in (b) (i.e. the probability that no more than four cases are reported in a particular year).

d) Calculate the distribution's standard deviation. Show the mean and standard deviation on one of the histograms in (c).

10. In a particular class, 65% of the students are men. The students have just written a test, and 55% of the students passed. Imagine randomly choosing one of the students: the probability that this student both passed and is male is 22%.

a) Construct a contingency table to display this information.

b) Randomly choose a student: the student turns out to be male. Calculate the probability that a student passed the test, given that the student is male.

c) Randomly choose a student; this student passed this test. Calculate the probability that a student is male, given that the student passed the test.

d) Calculate the probability that a randomly chosen student is a woman, given that the student passed.

e) Calculate the probability that a randomly chosen student passed the test, given that the student is a woman.

f) Are the test results and the gender of the students independent? Briefly and clearly explain your reasoning.

11. I have oversimplified the following situation, in order (I hope) to make a point.

Suppose the following:

a crime is committed in a city of one million adults;

the guilty party's DNA was found at the crime scene;

the probability that DNA taken from the actual criminal will be misread is zero (or the test's SENSITIVITY = 1);

the probability that a randomly chosen person's DNA will apparently match the criminal's DNA is 1 in a million (or the test's SPECIFICITY = 999,999/1,000,000);

the DNA of a suspect actually in custody matches the criminal's DNA;

the crown prosecutor alleges that, since the probability that the suspect's DNA could, by chance, match the criminal's DNA is 1 in a million, the probability that the suspect is innocent is 1 in a million.

a) Imagine testing ALL 1 million adults in this city (somewhat extreme and unrealistic). How many false positives would you expect?

b) How many true positives would you expect? (Hint: there is only one criminal.)

c) What fraction of the people who test positive (in (b) above) are guilty?

e) Calculate the probability that a suspect is guilty, given a positive test result.

f) Express what the prosecutor has claimed in the language of conditional probability.

12. Now try to make the previous situation a little more realistic.

The detainee was not tested at random, but the police have some reason to SUSPECT that this person MAY have committed the crime. Without DNA, what probability might the police claim for the detainee having committed the crime? This is a subjective, intuitive probability, but let's use 10%, or 0.1 for the police's estimate that the person is guilty. This doesn't sound very high, but it IS better than a probability of 1 in a million corresponding to picking an adult at random.

In addition, we will use more realistic values for the test's sensitivity and specificity. It turns out that human errors are the most significant contributors to tests' imperfections (e.g. mislabeling the sample, contaminating the sample). and it turns out that these errors are not too rare. Leonard Mlodinow (The Drunkard's Walk: How Randomness Rules Our Lives) claims that "many experts" think that the probability of human error in such cases is about 1%. Consequently, I will use a sensitivity of 0.99. This means that the probability of the test (humans effects included) matching two samples from the same person is 0.99.

I will also use a specificity of 0.99. This means that a sample NOT matching the crime-scene sample will be identified as a match 1% of the time (a false positive).

a) Treat the DNA test as a process with two independent trials: 1) choose a person (who could be guilty or not guilty); 2) test the person (the result could be a match [+] or not [-]). Construct a tree diagram. List all possible joint outcomes, and calculate their probabilities.

b) What is the (joint) probability that a person is guilty and tests positive?

c) What is the (joint) probability that a person is not guilty and tests positive?

d) What is the probability that a person will test positive?

e) What is the probability that a person tests positive, given that he is guilty? Express your answer using the conditional-probability notation.

f) What is the probability that the person is guilty, given that he tests positive? Express your answer using the conditional-probability notation.

g) Are the answers to (f) and (e) equal? Should they be equal?

h) Calculate the probability that a person tests negative, given that he is not guilty. Express your answer using the conditional-probability notation.

i) Calculate the probability that the person is not guilty, given a negative test. Express your answer using the conditional-probability notation.

j) Are the answers to (i) and (h) equal? Should they be equal?

13. The table below is the frequency distribution for the number of short-handed goals in the first 369 games of the 1993-1994 NHL season. This question investigates how well the number of short-handed goals is any game is described by a Poisson distribution. Spring 2010

Table I

Short-handed Goals

no. of goals	no. of games	P(x)	expected no. of games
0	291
1	67
2	10
3	1
4	0
5	0

(reading the tables: in 291games, there were no (0) short-handed goals; in 67 games, there was exactly one short-handed goal; etc. )

a) Calculate the mean number of SH goals per game.

b) Calculate the probability that, in a randomly selected game, there will be 0, 1, 2, 3, 4 short-handed goals, using the Poisson formula, and the mean calculated in (a).

c) Calculate the expected number of games in which 0, 1, 2, etc. short- handed goals are scored, using the probabilities calculated in (b), the mean calculated in (a), and a sample of 369 games

d) Calculate the standard deviation of this distribution using the data and either of the following equations. (P(x) stands for the probabilities calculated in (b).)