Reference no: EM135403

Q1.
In a pure exchange economy with two goods, G and H, two traders Amos and Elise, have Cobb-Douglas utility functions. Amos' utility is U_a = G^α_aH^1-α_a and Elise's utility is U_e = G^β_eH^1-β_e. Between them, they own 100 units of G and 50 units of H. Thus if Amos has G_a and H_a, Elise owns G_e =100 - G_a and H_e = 50 - H_a.
(a) Solve for their contract curve.
(b) Solve for their contract curve if α = β.
(c) Dropping the assumption α = β. find the competitive equilibrium prices.

Q2.
Consider an economy with no production. The economy is endowed with 50 bushels of alfalfa, a, and 50 bushels of barley, b. Two individuals, Mary and Larry, live in this economy and have the usual convex, negatively sloped indifference curves. Larry has an initial endowment with 50 bushels of alfalfa and no barley. Mary has no alfalfa and 50 bushels of barley. This initial endowment is not on the contract curve. At the initial endowment, Larry's utility function is U (a,b) = b + 2a and Mary's is U (a,b) = 2b +10a.

(a) If Mary offers a trade whereby she would give Larry three of her barley for one of his alfalfa, would Larry accept? Explain briefly. Illustrate your answer with an Edgeworth diagram. Show, on the same diagram, the set of efficient trades these individuals would rationally make.

(b) Now introduce prices. One of the points on the set of efficient trades you illustrated in your diagram will be a competitive equilibrium. Show such a point and illustrate the equilibrium price ratio p_a/ p_b.

Q3.

Consider the illustration below

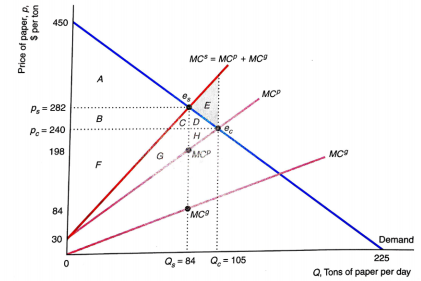
For the output market in this figure, what constant specific tax t on the output could the government set to maximize welfare?

Q4. Suppose that the inverse demand curve for paper is p = 200 - Q, the private marginal cost (unregulated competitive market supply) is MC^P= 80 +Q, and the marginal harm from pollution ("gunk") is MC^G= Q.

(a) What is the unregulated competitive equilibrium?
(b) What is the social optimum?
(c) What specific tax (per unit of output of gunk) results in the social optimum?

Q5.

Once upon a time, only two kinds of goods, wild boar and berries were available. Two individuals. Ayla and Durc, lived in a particular forest and had no access to neighbouring tribes. Ayla has the usual negatively sloped convex indifference curves. Durc, however, likes only wild board, but any berries he acquires can be costless fed to the snakes in the forest. There are 10 kgs of wild boar and 10 bushels of berries in the forest. Each individual is endowed with 5 units of each commidtiy.

(a) Show the initial situation in an Edgeworth box
(b) Show the set of all Pareto-efficient outcomes of trade.
(c) If Ayla and Durc end up at a Pareto-efficient allocation after a trade, will Durc be left with some of the berries? Explain, using a diagram.